Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A, Số có 4 chữ số có dạng: \(\overline{abcd}\)
\(a\) có 4 cách chọn
\(b\) có 1 cách chọn
\(c\) có 5 cách chọn
\(d\) có 5 cách chọn
Số các số có 4 chữ số mà chữ số hàng trăm bằng 8 là:
4 \(\times\) 1 \(\times\) 5 \(\times\) 5 = 100 (số)
B, Chữ số hàng chục thì có một thôi so có thể có 4 chữ số hàng chục bằng 3 được. em xem lại đề
C, Số có 4 chữ số có dạng: \(\overline{abcd}\)
\(a\) có 3 cách chọn
\(b\) có 3 cách chọn
\(c\) có 2 cách chọn
\(d\) có 2 cách chọn
Số số chẵn có 4 chữ số khác nhau được lập từ các chữ số đã cho là:
3 \(\times\) 3 \(\times\) 2 \(\times\) 2 = 36 (số)
Đáp số: A, 100 số
C, 36 số

Rồi nhá,gặp thánh rồi
1.Số tự nhiên là vĩnh cửu,không thể tìm ra một con số chính xác
2.(Tìm được,nhưng mình không giải được)
3.Như câu 1
4.Như câu 3
OK?

Cách 1: Chọn 3 làm chữ số hàng nghìn, ta có các số:
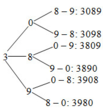
Nhìn vào sơ đồ trên ta thấy: Từ 4 chữ số đã cho ta viết được 6 số có chứ số hàng nghìn bằng 3 thoả mãn điều kiện của đề bài.
Chữ số 0 không thể đứng ở vị trí hàng nghìn. Vậy só các số thoả mãn điều kiện của đề bài là
6 × 3 = 18 (số)
Cách 2: Lần lượt chọn các chữ số hàng nghìn, hàng trăm, hàng chục và hàng đơn vị như sau:
- Có 3 cách chọn chữ số hàng nghìn của số thoả mãn điều kiện đề bài (vì số 0 không thể đứng ở vị trí hàng nghìn).
- Có 3 cách chọn chữ số hàng trăm (đó là 3 chữ số còn lại khác chữ số hàng nghìn)
- Có 2 cách chọn chữ số hàng chục (đó là 2 chữ số còn lại khác chữ số hàng nghìn và hàng trăm).
- Có 1 cách chọn chữ số hàng đơn vị (đó là chữ số còn lại khác hàng nghìn, hàng trăm và hàng chục).
Vậy các số viết được là:
3 × 3 × 2 × 1 = 18 (số)
b, Số lớn nhất có 4 chữ số khác nhau được viết từ 4 chữ số đã cho phải có chữ số hàng nghìn là chữ số lớn nhất (Trong 4 chữ số đã cho). Vậy chữ số hàng nghìn của số phải tìm bằng 9.
Chữ số hàng trăm phải là chữ số lớn nhất trong 3 chữ số còn lại. Vậy chữ số hàng trăm bằng 8.
Chữ số hàng chục là chữ số lớn trong 2 chữ số còn lại. Vậy chữ số hàng chục là 3.
Số phải tìm là 9830.
Tương tự phần trên ta nhận được số bé nhất thoả mãn điều kiện của đề bài là 3089.
c, Số lẻ lớn nhất thoả mãn điều kiện của đề bài phải có chữ số hàng nghìn là số lớn nhất trong 4 chữ số đã cho. Vậy chữ số hàng nghìn của số phải tìm bằng 9.
Số phải tìm có chữ số hàng nghìn bằng 9 và là số lẻ nên chữ số hàng đơn vị phải bằng 3.
Chữ số hàng trăm phải là chữ số lớn nhất trong hai chữ số còn lại, nên chữ số hàng trăm phải bằng 8.
Vậy số phải tìm là 9830.
Tương tự số chẵn nhỏ nhất là 3098.

Cách 1: Chọn 3 làm chữ số hàng nghìn, ta có các số:

Nhìn vào sơ đồ trên ta thấy: Từ 4 chữ số đã cho ta viết được 6 số có chứ số hàng nghìn bằng 3 thoả mãn điều kiện của đề bài.
Chữ số 0 không thể đứng ở vị trí hàng nghìn. Vậy só các số thoả mãn điều kiện của đề bài là
6 x 3 = 18 (số)
Cách 2: Lần lượt chọn các chữ số hàng nghìn, hàng trăm, hàng chục và hàng đơn vị như sau:
- Có 3 cách chọn chữ số hàng nghìn của số thoả mãn điều kiện đề bài (vì số 0 không thể đứng ở vị trí hàng nghìn).
- Có 3 cách chọn chữ số hàng trăm (đó là 3 chữ số còn lại khác chữ số hàng nghìn)
- Có 2 cách chọn chữ số hàng chục (đó là 2 chữ số còn lại khác chữ số hàng nghìn và hàng trăm).
- Có 1 cách chọn chữ số hàng đơn vị (đó là chữ số còn lại khác hàng nghìn, hàng trăm và hàng chục).
Vậy các số viết được là:
3 x 3 x 2 x 1 = 18 (số)
b, Số lớn nhất có 4 chữ số khác nhau được viết từ 4 chữ số đã cho phải có chữ số hàng nghìn là chữ số lớn nhất (Trong 4 chữ số đã cho). Vậy chữ số hàng nghìn của số phải tìm bằng 9.
Chữ số hàng trăm phải là chữ số lớn nhất trong 3 chữ số còn lại. Vậy chữ số hàng trăm bằng 8.
Chữ số hàng chục là chữ số lớn trong 2 chữ số còn lại. Vậy chữ số hàng chục là 3.
Số phải tìm là 9830.
Tương tự phần trên ta nhận được số bé nhất thoả mãn điều kiện của đề bài là 3089.
c, Số lẻ lớn nhất thoả mãn điều kiện của đề bài phải có chữ số hàng nghìn là số lớn nhất trong 4 chữ số đã cho. Vậy chữ số hàng nghìn của số phải tìm bằng 9.
Số phải tìm có chữ số hàng nghìn bằng 9 và là số lẻ nên chữ số hàng đơn vị phải bằng 3.
Chữ số hàng trăm phải là chữ số lớn nhất trong hai chữ số còn lại, nên chữ số hàng trăm phải bằng 8.
Vậy số phải tìm là 9830.
Tương tự số chẵn nhỏ nhất là 3098

2:
\(\overline{abcd}\)
d có 1 cách chọn
a có 3 cách chọn
b có 2 cách chọn
c có 1 cách chọn
=>Có 3*2*1*1=6 cách
1: \(\overline{abc}\)
a có 3 cách
b có 3 cách
c có 2 cách
=>Có 3*3*2=18 cách

a)18 trường hợp
b)số lớn nhất:9830,số bé nhất:3089
c)số lẻ lớn nhất:9803,số chẵn nhỏ nhất:3098

a) Gọi 4 chữ số đã cho là a;b;c;d
có thể lập được ít nhất 4 số từ 4 chữ số đó là: abcd; abdc; acbd; acdb;
b) Chọn chữ số hàng chục có 4 cách chọn
Chữ số hàng đơn vị có 3 cách chọn
=> có thể lập được 4 x 3 = 12 số có 2 chữ số từ 4 chữ số đã cho
TL:
a) Gọi 4 chữ số đã cho là a;b;c;d
Cách chọn chữ số hàng nghìn: 4 cách chọn
Cách chọn chữ số hàng trăm: 3 cách chọn
Cách chọn chữ số hàng chục: 2 cách chọn
Cách chọn chữ số hàng đơn vị: 1 cách chọn
Có thể lập được 4! số từ 4 chữ số
b) Chọn chữ số hàng chục có 4 cách chọn
Chữ số hàng đơn vị có 3 cách chọn
⇒ Có thể lập được 4×3=12 số có 2 chữ số từ 4 chữ số đã cho