giúp e vssss
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



5. ( - 199 ) + ( - 200 ) + ( - 201 )
= [ ( - 199 ) + ( - 20 ) ] + ( - 200 )
= ( - 400 ) + ( - 200 )
= - 600

12.
a. Do đường thẳng đi qua điểm A(-5;3) nên ta có:
\(-5a+b=3\) (1)
Do đường thẳng đi qua \(B\left(\dfrac{3}{2};-1\right)\) nên:
\(\dfrac{3}{2}a+b=-1\) (2)
Từ (1) và (2) ta có hệ: \(\left\{{}\begin{matrix}-5a+b=3\\\dfrac{3}{2}a+b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{8}{13}\\b=-\dfrac{1}{13}\end{matrix}\right.\)
b.
Gọi N là giao điểm (d1) và (d2), tọa độ N là nghiệm:
\(\left\{{}\begin{matrix}2x+5y=17\\4x-10y=14\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=6\\y=1\end{matrix}\right.\) \(\Rightarrow N\left(6;1\right)\)
Do đường thẳng đi qua M(9;-6) nên:
\(9a+b=-6\)
Do đường thẳng đi qua N(6;1) nên:
\(6a+b=1\)
Ta được hệ: \(\left\{{}\begin{matrix}9a+b=-6\\6a+b=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{7}{3}\\b=15\end{matrix}\right.\)
13.
a.
Hai đường thẳng cắt nhau tại 1 điểm trên trục tung khi hoành độ giao điểm bằng 0
Tọa độ giao điểm 2 đường thẳng là nghiệm của hệ:
\(\left\{{}\begin{matrix}5x-2y=3\\x+y=m\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}5x-2y=3\\2x+2y=2m\end{matrix}\right.\)
\(\Rightarrow7x=2m+3\)
\(\Rightarrow x=\dfrac{2m+3}{7}\)
Hai đường thẳng cắt nhau trên trục tung nên:
\(\dfrac{2m+3}{7}=0\Rightarrow m=-\dfrac{3}{2}\)
Em tự vẽ hình
b.
Hai đường thẳng cắt nhau tại 1 điểm trên trục hoành khi tung độ giao điểm bằng 0.
Tọa độ giao điểm 2 đường thẳng là nghiệm:
\(\left\{{}\begin{matrix}mx+3y=10\\x-2y=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}mx+3y=10\\mx-2my=4m\end{matrix}\right.\)
Trừ vế cho vế \(\Rightarrow\left(2m+3\right)y=10-4m\)
2 đường thẳng cắt nhau khi \(2m+3\ne0\Rightarrow m\ne-\dfrac{3}{2}\)
Khi đó tung độ giao điểm là: \(y=\dfrac{10-4m}{2m+3}\)
2 đường cắt nhau trên trục hoành khi:
\(\dfrac{10-4m}{2m+3}=0\Rightarrow10-4m=0\)
\(\Rightarrow m=\dfrac{5}{2}\)

\(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{z}{5}=\dfrac{6x}{9}=\dfrac{6y}{8}=\dfrac{6z}{30}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{6x}{9}=\dfrac{6y}{8}=\dfrac{6z}{30}=\dfrac{6\left(x+y+z\right)}{9+8+30}=\dfrac{6.20}{47}=\dfrac{120}{47}\\ \Rightarrow x=\dfrac{120}{47}.3:2=\dfrac{180}{47}\\ \Rightarrow y=\dfrac{120}{47}.4:3=\dfrac{160}{47}\\ \Rightarrow z=\dfrac{120}{47}.5=\dfrac{600}{47}\)
Bạn xem xem cách này có đúng không nha!

`a,b,c` lập thành CSC `=>a+c=2b`
Thay `a+c=2b` vào `a+b+c=15` có: `2b+b=15<=>b=5`
`=>a+c=2.5=10=>a=10-c`
Thay `b=5` vào `1/a+1/b+1/c=71/105` có:
`1/a+1/5+1/c=71/105`
`<=>1/a+1/c=10/21`
`<=>21a+21c=10ac` `(1)`
Thay `a=10-c` vào `(1)` có: `21(10-c)+21c=10(10-c)c`
`<=>[(c=3),(c=7):}=>[(a=7),(a=3):}`
KL: `[(a=7;b=5;c=3),(a=3;b=5;c=7):}`

Câu 1:
BC vuông góc SA
BC vuông góc BA
=>BC vuông góc (SAB)
=>BC vuông góc SB
=>ΔSBC vuông tại B
CD vuông góc SA
DC vuông góc AD
=>DC vuông góc (SAD)
=>DC vuông góc SD
=>ΔDCS vuông tại D
Câu 2:
CD vuông góc (SAD)
AH vuông góc (SAD)
=>CD vuông góc AH
mà AH vuông góc SD
nên AH vuông góc (SCD)
=>AH vuông góc SC



3x-8 chia hết cho x+1
=> 3(x+1)-11 chia hết cho x+1
=> 11 chia hết cho x+1
=> x+1 thuộc Ư(11)={1;-1;11;-11}
=> x thuộc {0;-2;10;-12}
Ta có:
3x - 8 = 3x + 3 - 11 = 3(x + 1) - 11
Để (3x - 8) ⋮ (x - 1) thì 11 ⋮ (x - 1)
⇒ x - 1 ∈ Ư(11) = {-11; -1; 1; 11}
⇒ x ∈ {-10; 0; 2; 12}
(Nếu chỉ tìm x là số tự nhiên thì x ∈ {2; 12})

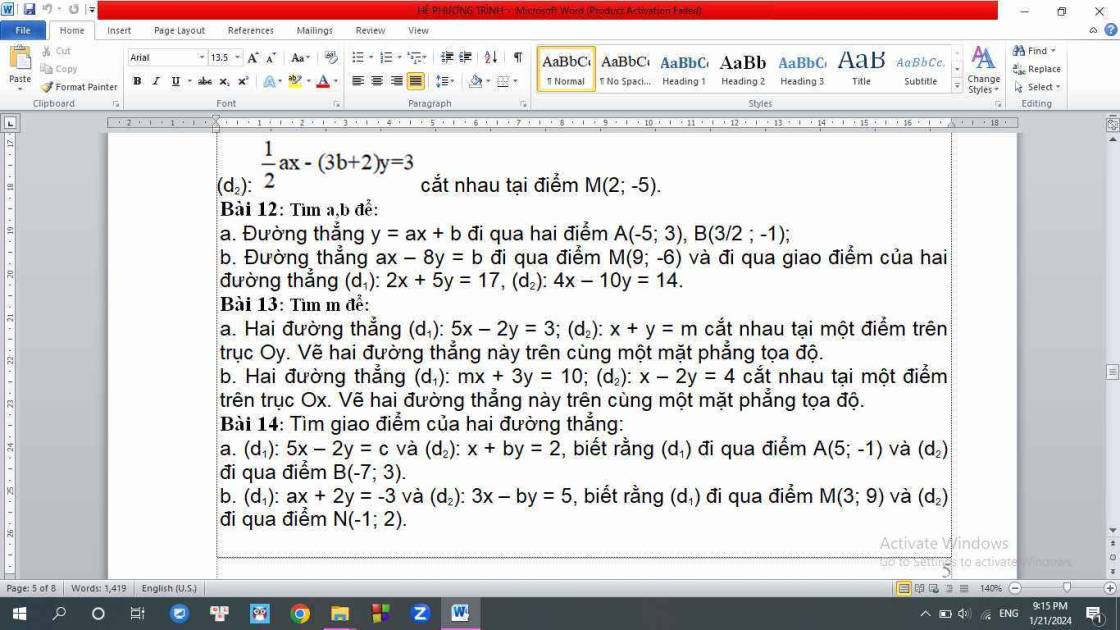 cứu e vssss
cứu e vssss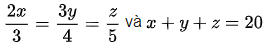





39. It is raining so we can't go to the beach.
40. If they liked this house, they would buy it.
41. Hurry up or we will be late.
42. They take pride of their school uniform.
43. Why don't we go out for a walk?