
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các câu hỏi dưới đây có thể giống với câu hỏi trên
 cứu e vssss
cứu e vssss
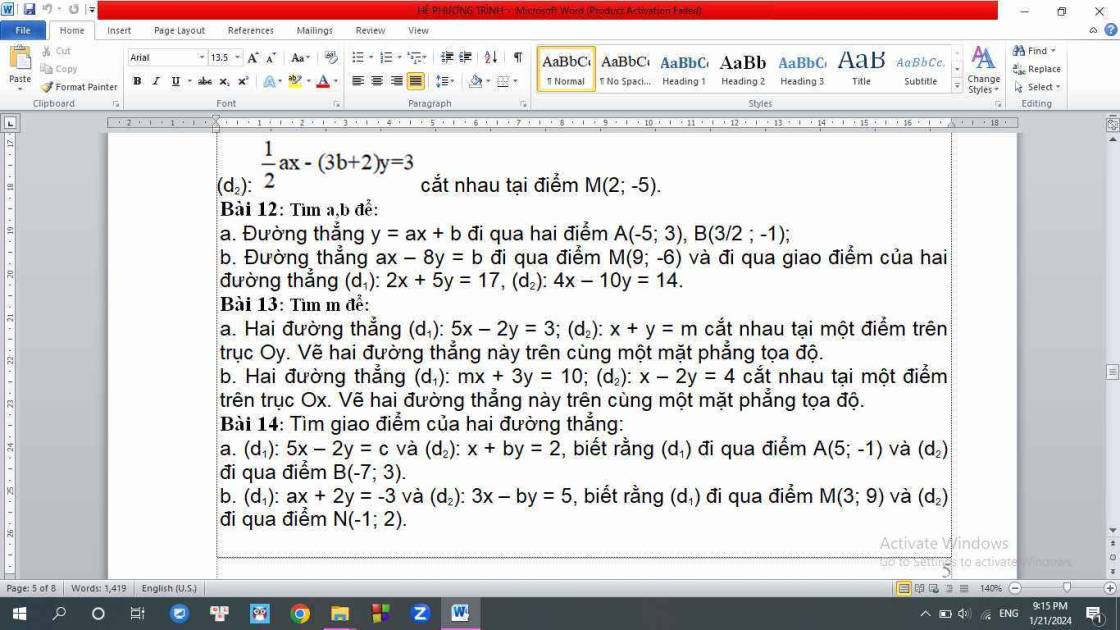
12.
a. Do đường thẳng đi qua điểm A(-5;3) nên ta có:
\(-5a+b=3\) (1)
Do đường thẳng đi qua \(B\left(\dfrac{3}{2};-1\right)\) nên:
\(\dfrac{3}{2}a+b=-1\) (2)
Từ (1) và (2) ta có hệ: \(\left\{{}\begin{matrix}-5a+b=3\\\dfrac{3}{2}a+b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{8}{13}\\b=-\dfrac{1}{13}\end{matrix}\right.\)
b.
Gọi N là giao điểm (d1) và (d2), tọa độ N là nghiệm:
\(\left\{{}\begin{matrix}2x+5y=17\\4x-10y=14\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=6\\y=1\end{matrix}\right.\) \(\Rightarrow N\left(6;1\right)\)
Do đường thẳng đi qua M(9;-6) nên:
\(9a+b=-6\)
Do đường thẳng đi qua N(6;1) nên:
\(6a+b=1\)
Ta được hệ: \(\left\{{}\begin{matrix}9a+b=-6\\6a+b=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{7}{3}\\b=15\end{matrix}\right.\)
13.
a.
Hai đường thẳng cắt nhau tại 1 điểm trên trục tung khi hoành độ giao điểm bằng 0
Tọa độ giao điểm 2 đường thẳng là nghiệm của hệ:
\(\left\{{}\begin{matrix}5x-2y=3\\x+y=m\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}5x-2y=3\\2x+2y=2m\end{matrix}\right.\)
\(\Rightarrow7x=2m+3\)
\(\Rightarrow x=\dfrac{2m+3}{7}\)
Hai đường thẳng cắt nhau trên trục tung nên:
\(\dfrac{2m+3}{7}=0\Rightarrow m=-\dfrac{3}{2}\)
Em tự vẽ hình
b.
Hai đường thẳng cắt nhau tại 1 điểm trên trục hoành khi tung độ giao điểm bằng 0.
Tọa độ giao điểm 2 đường thẳng là nghiệm:
\(\left\{{}\begin{matrix}mx+3y=10\\x-2y=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}mx+3y=10\\mx-2my=4m\end{matrix}\right.\)
Trừ vế cho vế \(\Rightarrow\left(2m+3\right)y=10-4m\)
2 đường thẳng cắt nhau khi \(2m+3\ne0\Rightarrow m\ne-\dfrac{3}{2}\)
Khi đó tung độ giao điểm là: \(y=\dfrac{10-4m}{2m+3}\)
2 đường cắt nhau trên trục hoành khi:
\(\dfrac{10-4m}{2m+3}=0\Rightarrow10-4m=0\)
\(\Rightarrow m=\dfrac{5}{2}\)