PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
2 tháng 10 2019
Phương trình x + 2 = 0 có nghiệm x = -2.
Phương trình 
có nghiệm duy nhất x = -2 khi -2m + 3m – 1 = 0 suy ra m = 1.
Vậy hai phương trình tương đương khi m = 1.
PT
1
CM
28 tháng 5 2017
Suy ra x = 1 và x = -4 là nghiệm của phương trình m x 2 - 4 x - m + 4 = 0
CM
3 tháng 8 2017
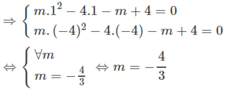
3x - 1 = 0 ⇔ x = 1/3
Suy ra x = 1/3 là nghiệm của phương trình
PT
1
CM
1 tháng 4 2018
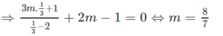
Phương trình 3x – 2 = 0 có nghiệm x = 2/3, thay x = 2/3 vào phương trình
(m + 3)x - m + 4 = 0 , ta có
2(m + 3) / 3 - m + 4 = 0
⇔ -m / 3 + 6 = 0 ⇔ m = 18
Với m = 18 phương trình (m + 3)x - m + 4 = 0 trở thành 21x = 14 hay x = 2/3
Vậy hai phương trình tương đương khi m = 18.
PT
1
CM
2 tháng 7 2017
Phương trình x + 2 = 0 có nghiệm x = -2. Thay x = -2 vào phương trình
m ( x 2 + 3 x + 2 ) + m 2 x + 2 = 0 , ta có
-2m2 + 2 = 0 ⇔ m = 1 hoặc m = -1
Khi m = 1 phương trình thứ hai trở thành
x 2 + 4 x + 4 = 0
⇔ x = -2
Khi m = -1 phương trình thứ hai trở thành
- x 2 - 2 x = 0
⇔ -x(x + 2) = 0
Phương trình này có hai nghiệm x = 0 , x = -2.
Vậy hai phương trình đã cho tương đương khi m = 1.
CM
1 tháng 11 2018
Ta có (1) ⇔ x - 1 m x - m + 2 = 0 ⇔ x = 1 m x − m + 2 = 0
Do hai phương trình tương đương nên x = 1 cũng là nghiệm của phương trình (2)
Thay x = 1 vào (2), ta được
m - 2 - 3 + m 2 - 15 = 0 ⇔ m 2 + m - 20 = 0 ⇔ m = − 5 m = 4
Với m = −5, ta có
(1) trở thành - 5 x 2 + 12 x - 7 = 0 ⇔ x = 7 5 hoặc x = 1
(2) trở thành - 7 x 2 - 3 x + 10 = 0 ⇔ x = - 10 7 hoặc x = 1
Suy ra hai phương trình không tương đương
Với m = 4, ta có
(1) trở thành 4 x 2 - 6 x + 2 = 0 ⇔ x = 1 2 hoặc x = 1
(2) trở thành 2 x 2 - 3 x + 1 = 0 ⇔ x = 1 2 hoặc x = 1
Suy ra hai phương trình tương đương.
Vậy m = 4 thỏa mãn.
Đáp án cần chọn là: C
CM
22 tháng 10 2019
- Ta có (2) ⇔ x + 2 2 x 2 + m x - 2 = 0 ⇔ x = − 2 2 x 2 + m x − 2 = 0
Do hai phương trình tương đương nên x = −2 cũng là nghiệm của phương trình (1)
- Thay x = −2 vào (1), ta được 2 - 2 2 + m - 2 - 2 = 0 ⇔ m = 3.
- Với m = 3, ta có:
...(1) trở thành 2 x 2 + 3 x - 2 = 0 ⇔ x = - 2 hoặc x = 1 2
...(2) trở thành 2 x 3 + 7 x 2 + 4 x - 4 = 0 ⇔ x + 2 2 2 x + 1 = 0 ⇔ x = - 2 hoặc x = 1 2
Suy ra hai phương trình tương đương.
Vậy m = 3 thỏa mãn.
Đáp án cần chọn là: B
BT
3 tháng 5 2017
a) \(x+2=0\Leftrightarrow x=-2\)
Phương trình: \(\dfrac{mx}{x+3}=3m-1\) (*) có đkxđ: \(x\ne-3\)
Vì cặp phương trình tương đương nên phương trình (*) có nghiệm là x = -2:
\(\dfrac{2m}{2+3}+3m-1=0\) \(\Leftrightarrow\dfrac{2m}{5}+3m=1\)\(\Leftrightarrow m\left(\dfrac{2}{5}+3\right)=1\)
\(\Leftrightarrow\dfrac{17}{5}m=1\) \(m=\dfrac{5}{17}\)
Vậy \(m=\dfrac{5}{17}\) thì hai phương trình tương đương.
BT
3 tháng 5 2017
b) Pt (1) \(x^2-9=0\) có hai nghiệm là: \(x=3;x=-3\).
Để cặp phương trình tương đương thì phương trình (2) \(2x^2+\left(m-5\right)x-3\left(m+1\right)=0\) có nghiệm là: \(x=3;x=-3\).
Suy ra: \(\left\{{}\begin{matrix}2.3^2+\left(m-5\right).3-3.\left(m+1\right)=0\\2.\left(-3\right)^2+\left(m-5\right).\left(-3\right)-3.\left(m+1\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}0=0\\30-6m=0\end{matrix}\right.\) \(\Leftrightarrow m=5\)
Vậy m = 5 thì hai phương trình tương đương.
CM
7 tháng 4 2017
Xét các đáp án:
- Đáp án A.
Điều kiện: x – 1 ≥ 0 ⇔ x ≥ 1.
Khi đó x + x − 1 = 1 + x − 1 ⇔ x = 1(TM).
Do đó phương trình có nghiệm x = 1 và hai phương trình x + x − 1 = 1 + x − 1 và
x = 1 tương đương.
- Đáp án B. Ta có: x + x − 2 = 1 + x − 2 ⇔ x − 2 ≥ 0 x = 1 ⇒ x ∈ ∅
Do đó, x + x − 2 = 1 + x − 2 và x = 1 không phải là cặp phương trình tương đương
- Đáp án C. Ta có: x x + 2 = x ⇔ x ≥ 0 x = 0 x + 2 = 1 x + 2 = 1 ⇔ x = − 1 ⇔ x = 0
Do đó, x(x + 2) = x và x + 2 = 1 không phải là cặp phương trình tương đương
- Đáp án D. Ta có: x ( x + 2 ) = x ⇔ x = 0 x = − 1 x + 2 = 1 ⇔ x = − 1
Do đó, x(x + 2) = x và x + 2 = 1 không phải là cặp phương trình tương đương
Đáp án cần chọn là: A
Phương trình x 2 - 9 = 0 có hai nghiệm x =3 và x =-3
Giá trị x = 3 là nghiệm của phương trình
2 x 2 + (m - 5)x - 3(m + 1) = 0
Khi 18 + 3(m - 5) - 3(m + 1) = 0
Đẳng thức trên thỏa mãn với mọi m.
Giá trị x = -3 là nghiệm của hệ phương trình (1) khi
18 + 3(m - 5) - 3(m + 1) = 0
⇔ 30 - 6m = 0 ⇔ m = 5
Khi m = 5 phương trình (1) trở thành
2 x 2 - 18 = 0 ⇔ x 2 - 9 = 0
Phương trình này có hai nghiệm x = 3 và x = -3.
Vậy với m = 5 hai phương trình đã cho tương đương.