Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

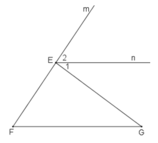
Kẻ tia En song song với FG.
∠F và ∠E2 ở vị trí đồng vị ⇒ ∠F = ∠E2. (1)
∠G và ∠E1 ở vị trí so le trong ⇒ ∠G = ∠E1. (2)
Từ (1) và (2) suy ra: ∠F + ∠G = ∠E1 + ∠E2 (đpcm).
Hay ∠EFG + ∠EGF = ∠GEm.

Tổng 3 góc tam giác = 180 độ => góc FEG = 180 độ - FEG - EGF
Mà FEG và GEm bù nhau => FEG = 180 độ - GEm => EFG + EGF = GEm

Bài giải
Ta có : \(BC\text{ }//\text{ }Az\) nên \(\widehat{C_2}=\widehat{A_2}\) ( hai góc so le trong )
Mà \(\widehat{CAx}=\widehat{A_2}+\widehat{A_3}\) là góc ngoài tại đỉnh A của \(\Delta ABC\) nên \(\widehat{A_2}+\widehat{A_3}=\widehat{B}+\widehat{C_2}\)
lại có : \(\widehat{B}=\widehat{C_2}=\widehat{A_2}\) nên \(\widehat{A_3}=\widehat{B}=\widehat{C_2}=\widehat{A_2}\)
Vì \(\widehat{A_2}=\widehat{A_3}\) nên Az là tia phân giác \(\widehat{CAx}\)

Để chứng minh rằng 2 tia phân giác 2 góc đối đỉnh là 2 tia đối nhau, chúng ta cần sử dụng một số khái niệm và định lý trong hình học. Dưới đây là cách chứng minh:
Giả sử chúng ta có hai tia AB và AC, và chúng phân giác hai góc đối đỉnh, tức là góc BAC và góc CAD. Chúng ta cần chứng minh rằng hai tia AB và AC là hai tia đối nhau.
Để chứng minh điều này, ta sẽ sử dụng Định lý Tia Phân Giác (Bisector Theorem) và Định lý Tia Tiếp Tuyến (Alternate Segment Theorem) như sau:
Bước 1: Vẽ đường thẳng đi qua điểm A và song song với tia BC (đường thẳng đó gọi là đường thẳng d).
Bước 2: Do AB là tia phân giác góc BAC, nên theo Định lý Tia Phân Giác, ta có: AB/BD = AC/CD
Bước 3: Do AC là tia phân giác góc CAD, nên theo Định lý Tia Phân Giác, ta có: AC/CD = AB/BD
Bước 4: Từ Bước 2 và Bước 3, ta có: AB/BD = AC/CD = AB/BD Bước 5: Từ Bước 4, ta suy ra AB = AC.
Vậy, chúng ta đã chứng minh rằng hai tia AB và AC là hai tia đối nhau. Hy vọng cách chứng minh trên giúp bạn hiểu và giải đúng bài tập.
Để chứng minh rằng 2 tia phân giác 2 góc đối đỉnh là 2 tia đối nhau, chúng ta cần sử dụng một số khái niệm và định lý trong hình học. Dưới đây là cách chứng minh:
Giả sử chúng ta có hai tia AB và AC, và chúng phân giác hai góc đối đỉnh, tức là góc BAC và góc CAD. Chúng ta cần chứng minh rằng hai tia AB và AC là hai tia đối nhau.
Để chứng minh điều này, ta sẽ sử dụng Định lý Tia Phân Giác (Bisector Theorem) và Định lý Tia Tiếp Tuyến (Alternate Segment Theorem) như sau:
Bước 1: Vẽ đường thẳng đi qua điểm A và song song với tia BC (đường thẳng đó gọi là đường thẳng d).
Bước 2: Do AB là tia phân giác góc BAC, nên theo Định lý Tia Phân Giác, ta có: AB/BD = AC/CD
Bước 3: Do AC là tia phân giác góc CAD, nên theo Định lý Tia Phân Giác, ta có: AC/CD = AB/BD
Bước 4: Từ Bước 2 và Bước 3, ta có: AB/BD = AC/CD = AB/BD Bước 5: Từ Bước 4, ta suy ra AB = AC.
Vậy, chúng ta đã chứng minh rằng hai tia AB và AC là hai tia đối nhau. Hy vọng cách chứng minh trên giúp bạn hiểu và giải đúng bài tập.


*Vẽ các trung tuyến BN, CE lần lượt tại B và C. Gọi G là trọng tâm của \(\Delta ABC\)..Nối MN
Áp dụng BĐT tam giác vào \(\Delta AMN\), ta được:
\(AM< AN+NM\)(1)
Mà \(AN=\frac{1}{2}AC\)(Do BN là trung tuyến ứng với cạnh AC) (2)
và \(MN=\frac{1}{2}AB\)(Do MN là đường trung bình ứng với cạnh \(AB\)của \(\Delta ABC\)) (3)
Từ (1), (2) và (3) suy ra \(AM< \frac{1}{2}AB+\frac{1}{2}AC\)
hay \(AM< \frac{1}{2}\left(AB+AC\right)\) (đpcm)
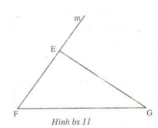
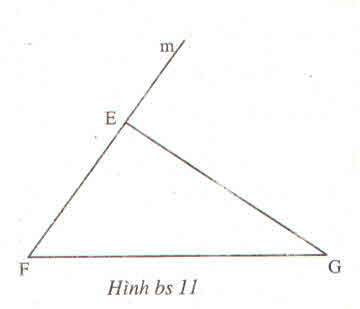

Cậu cầu cứu ai đi ....😅😅😅😅
Tớ cũng đg tìm bài này ...hehe 😁😁😁😁
EFG
+
EGF
=
GEm
suy ra G+F=m dư 1
m+1=E
mình nói đến đây thôi nha vì mình học lớp 6