

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



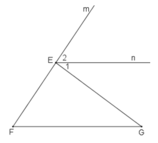
Kẻ tia En song song với FG.
∠F và ∠E2 ở vị trí đồng vị ⇒ ∠F = ∠E2. (1)
∠G và ∠E1 ở vị trí so le trong ⇒ ∠G = ∠E1. (2)
Từ (1) và (2) suy ra: ∠F + ∠G = ∠E1 + ∠E2 (đpcm).
Hay ∠EFG + ∠EGF = ∠GEm.

EFG
+
EGF
=
GEm
suy ra G+F=m dư 1
m+1=E
mình nói đến đây thôi nha vì mình học lớp 6

Tổng 3 góc tam giác = 180 độ => góc FEG = 180 độ - FEG - EGF
Mà FEG và GEm bù nhau => FEG = 180 độ - GEm => EFG + EGF = GEm

a) Ta có: + \(\widehat{BOC}\)là góc ngoài của tam giác OBK
=> \(\widehat{BOC}=\widehat{OBK}+\widehat{OKB}\) (1)
+ \(\widehat{OKB}\)là góc ngoài của tam giác AKC
=>\(\widehat{OKB}=\widehat{A}+\widehat{ACK}\)(2)
Từ (1)(2) =>\(\widehat{BOC}=\widehat{OBK}+\widehat{A}+\widehat{ACK}\)
hay\(\widehat{BOC}=\widehat{A}+\widehat{ABO}+\widehat{ACO}\)
b) Ta có:\(\widehat{ABO}+\widehat{ACO}=90^o-\frac{\widehat{A}}{2}\)
=>\(2\widehat{ABO}+2\widehat{ACO}=180^o-\widehat{A}\)(3)
Xét tam giác ABC có:
\(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^o\)( Tổng 3 góc trong 1 tam giác)
=>\(\widehat{ABC}+\widehat{ACB}=180^o-\widehat{A}\)(4)
Từ (3)(4) => \(2\widehat{ABO}+2\widehat{ACO}=\widehat{ABC}+\widehat{ACB}\)(*)
Ta có: BO là tia phân giác của góc ACB
=>\(2\widehat{ABO}=\widehat{ABC}\)(**)
Từ (*)(**) => \(2\widehat{ABO}+2\widehat{ACO}=2\widehat{ABO}+\widehat{ACB}\)
=>\(2\widehat{ACO}=\widehat{ACB}\)
=> CO là tia phân giác của góc ACB

nhanh lên mình cần gấp lắm
giúp mình với huhuhuhuhuhuhuhuhuhuhuhuhuhuhuhuhuhu

Ta có: \(\widehat {ACB} + \widehat {ACx} = {180^o}\, \Rightarrow \widehat {ACx} = 180 - \widehat {ACB}\)
\(\widehat {BAC} + \widehat {CBA} + \widehat {ACB} = {180^o} \Rightarrow \widehat {BAC} + \widehat {CBA} = {180^o} - \widehat {ACB}\)
Vậy \(\widehat {ACx} = \widehat {BAC} + \widehat {CBA}\)