PP
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
S
29 tháng 12 2020
a) \(\dfrac{a}{5}=\dfrac{b}{4}\Rightarrow\dfrac{a^2}{25}=\dfrac{b^2}{16}\)
Áp dụng tính chất DTSBN :
\(\dfrac{a^2}{25}=\dfrac{b^2}{16}=\dfrac{a^2-b^2}{25-16}=\dfrac{1}{9}\)
\(\Rightarrow\left\{{}\begin{matrix}a^2=\dfrac{1}{9}\cdot25=\dfrac{25}{9}\\b^2=\dfrac{1}{9}\cdot16=\dfrac{16}{9}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{5}{3};b=\dfrac{4}{3}\\a=\dfrac{-5}{3};b=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy \(\left(a;b\right)\in\left\{\left(\dfrac{5}{3};\dfrac{4}{3}\right);\left(-\dfrac{5}{3};-\dfrac{4}{3}\right)\right\}\)
b) \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\Rightarrow\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{c^2}{16}\)
Áp dụng tính chất DTSBN :
\(\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{c^2}{16}=\dfrac{2c^2}{32}=\dfrac{a^2-b^2+2c^2}{4-9+32}=\dfrac{108}{27}=4\)
\(\Rightarrow\left\{{}\begin{matrix}a^2=4.4=16\\b^2=4.9=36\\c^2=4,16=64\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=4;=6;c=8\\a=-4;b=-6;c=-8\end{matrix}\right.\)
Vậy (a;b;c) \(\in\left\{\left(4;6;8\right);\left(-4;-6;-8\right)\right\}\)
T
2
2 tháng 11 2021
Sửa \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\)
Đặt \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=k\Rightarrow a=2k;b=3k;c=4k\)
\(a^2-b^2+2c^2=108\\ \Rightarrow4k^2-9k^2+32k^2=108\\ \Rightarrow27k^2=108\Rightarrow k^2=4\\ \Rightarrow\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=4;y=6;z=8\\x=-4;y=-6;z=-8\end{matrix}\right.\)
TH
2 tháng 11 2021
Ta có:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a^2}{2^2}=\dfrac{b^2}{3^2}=\dfrac{2c^2}{2.4^2}=\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{2c^2}{32}\)
Áp dụng tcdtsbn , ta có:
\(\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{2c^2}{32}=\dfrac{a^2-b^2+2c^2}{4-9+32}=\dfrac{108}{27}=4\)
\(\Rightarrow\left\{{}\begin{matrix}a=8\\b=12\\c=16\end{matrix}\right.\)
PT
1
CM
20 tháng 1 2018
Ta có:
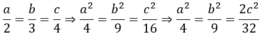
Theo tính chất dãy tỉ số bằng nhau ta có:
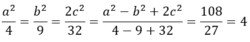
Ta có:
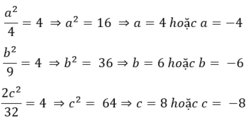
Mà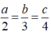 
nên a, b và c cùng dấu.
Vậy ta tìm được các số a1 = 4; b1 = 6; c1 = 8 hoặc a2 = -4; b2 = -6 và c2 = -8
TD
1
2 tháng 11 2017
Theo đề bài ta có :
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4};a^2-b^3-c^4=108\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a^2-b^3-c^4}{4-27-256}=\frac{108}{-279}=\frac{-12}{31}\)
\(\Rightarrow\)\(a=\frac{-12}{31}.2=\frac{-24}{31}\)
\(\Rightarrow\)\(b=\frac{-12}{31}.3=\frac{-36}{31}\)
\(\Rightarrow\)\(c=\frac{-12}{31}.4=\frac{-48}{31}\)
Vậy bạn tự kết luận
28 tháng 10 2021
tham khảo!!
https://lazi.vn/edu/exercise/tim-cac-so-a-b-c-biet-rang-a-2-b-3-c-4-va-a-2-b-2-2c-2-108
MT
1
11 tháng 8 2019
Ta có : \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\Rightarrow\frac{a^2}{4}=\frac{b^2}{9}=\frac{c}{4}=\frac{a^2-b^2+c}{4-9+4}=\frac{108}{-1}=-108\)
a,b không tìm được bạn à vì có dấu âm,c thì tìm được
Bạn có chắc ghi sai đề ko
DT
5
NH
7 tháng 7 2019
Ta có: \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\Leftrightarrow\frac{a^2}{4}=\frac{b^2}{9}=\frac{2c^2}{32}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a^2}{4}=\frac{b^2}{9}=\frac{2c^2}{32}=\frac{a^2-b^2+2c^2}{4-9+32}=\frac{108}{27}=4\)
\(\Rightarrow\hept{\begin{cases}\frac{a}{2}=4\\\frac{b}{3}=4\\\frac{c}{4}=4\end{cases}\Rightarrow}\hept{\begin{cases}a=8\\b=12\\c=16\end{cases}}\)
Vậy...
7 tháng 7 2019
TA CÓ:\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\)
\(\Leftrightarrow\frac{a^2}{4}=\frac{b^2}{9}=\frac{c^2}{16}\)
\(\Leftrightarrow\frac{a^2}{4}=\frac{b^2}{9}=\frac{2c^2}{32}\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\frac{a^2}{4}=\frac{b^2}{9}=\frac{2c^2}{32}=\frac{a^2-b^2+2c^2}{4-9+32}=\frac{108}{27}=4\)
\(\cdot\frac{a^2}{4}=4\Leftrightarrow a^2=16\Leftrightarrow a=\pm4\)
\(\cdot\frac{b^2}{9}=4\Leftrightarrow b^2=36\Leftrightarrow b=\pm6\)
\(\cdot\frac{2c^2}{32}=4\Leftrightarrow2c^2=128\Leftrightarrow c^2=64\Leftrightarrow c=\pm8\)
Vậy các cặp \(\left(a,b,c\right)\)thõa mãn là : \(\left(4;6;8\right)\)và \(\left(-4;-6;-8\right)\)
MT
1
11 tháng 8 2019
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\Rightarrow\frac{a^2}{4}=\frac{b^2}{9}=\frac{c^2}{16}\Rightarrow\frac{a^2}{4}=\frac{b^2}{9}=\frac{2c^2}{32}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a^2}{4}=\frac{b^2}{9}=\frac{2c^2}{32}=\frac{a^2-b^2+2c^2}{4-9+32}=\frac{108}{27}=4\)
=> \(\hept{\begin{cases}\frac{a^2}{4}=4\\\frac{b^2}{9}=4\\\frac{c^2}{16}=4\end{cases}}\Rightarrow\hept{\begin{cases}a^2=16\\b^2=36\\c^2=64\end{cases}\Rightarrow}\hept{\begin{cases}a=\pm4\\b=\pm6\\c=\pm8\end{cases}}\)
LT
1
6 tháng 10 2016
Đặt \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=k\)
=> \(\begin{cases}a=2k\\b=3k\\c=4k\end{cases}\)
Vì a2 - b2 + 2c2 = 108 => 4k2 - 9k2 + 32k2 =>27k2 = 108
=> k = \(\pm\)2
Với k = 2 => \(\begin{cases}a=4\\b=6\\c=8\end{cases}\)
Với k = -2 => \(\begin{cases}a=-4\\b=-6\\c=-8\end{cases}\)
