Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tg ABC ( ^A = 90o ) có:
BC2 = AB2 + AC2 (định lý Pytago)
Thay số: BC2 = 3,752 + 4,52
BC2 = 14,0625 + 20,25
BC2 = 34,3125
BC = \(\sqrt{34,3125}\) (BC > 0)
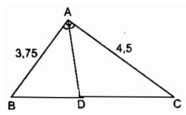
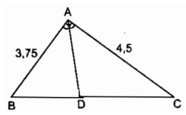
Xét tg ABC có D là đường pg ^A ( gt )
=> \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)
<=> \(\dfrac{AB}{AC+AB}=\dfrac{BD}{CD+BD}\)
Thay số: \(\dfrac{3,75}{4,5+3,75}=\dfrac{BD}{BC}\)
<=> \(\dfrac{3,75}{8,25}=\dfrac{BD}{\sqrt{34,3125}}\)
=> BD = (cm)
=> CD = BC - CD = (cm)

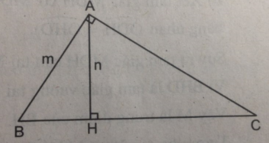
Xét hai tam giác ABC và HBA, ta có: ∠ BAC = ∠ BHA = 1v
Góc B là góc nhọn chung
Vậy △ ABC đồng dạng △ HBA
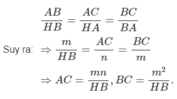
Xét tam giác vuông ABH, ta có:
HB = √ A B 2 - A H 2 = m 2 - n 2
Từ đó, ta có: 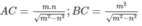
Với m = 12,5cm, n = 10,85cm, ta tính được:
AC ≈ 21,85cm; BC ≈ 25,17cm.

mình nghĩ nên đẩy ý b) lên trước vì đã tính AC đâu mà có tỉ số :D
a) Áp dụng định lí Pythagoras cho ΔvuôngABC ta có :
BC2 = AB2 + AC2
=> \(AC=\sqrt{BC^2-AB^2}=\sqrt{15^2-9^2}=12\left(cm\right)\)
b) Tỉ số hai đoạn thẳng AB và AC : AB/AC = 9/12 = 3/4
c) Vì CD là phân giác của ^C nên theo tính chất đường phân giác trong tam giác ta có : \(\frac{AD}{AC}=\frac{BD}{BC}\)
Áp dụng tính chất dãy tí số bằng nhau ta có : \(\frac{AD}{AC}=\frac{BD}{BC}=\frac{AD+BD}{AC+BC}=\frac{AB}{AC+BC}=\frac{9}{12+15}=\frac{1}{3}\)
=> \(\hept{\begin{cases}\frac{AD}{AC}=\frac{1}{3}\\\frac{BD}{BC}=\frac{1}{3}\end{cases}}\Rightarrow\hept{\begin{cases}AD=\frac{1}{3}AC=4\left(cm\right)\\BC=\frac{1}{3}BC=5\left(cm\right)\end{cases}}\)

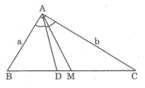
Với a = 4,15 (cm); b = 7,25 (cm), sử dụng máy tỉnh, ta tính được:
BC = 8,35 cm
BD = 3,04 cm
DC ≈ 5,31 cm
AM ≈ 4,18 cm
DM ≈ 1,14cm



Chọn C