Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = a 2 + b 2
Suy ra: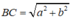
Ta có: AM = BM = 1/2.BC (tính chất đường trung tuyến ứng với cạnh huyền).
Suy ra: AM = 1/2 a 2 + b 2
Vì AD là đường phân giác của ∠(BAC) nên:
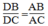(tính chất đường phân giác)
Suy ra: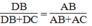 
hay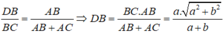 
Vậy
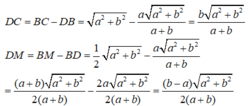
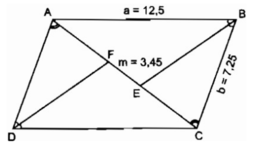
Vì ABCD là hình bình hành nên ∠ ABC = ∠ ADC.
Mặt khác, BE và DF lần lượt là phân giác của các góc B và D, do đó suy ra ∠ ADF = ∠ CBE
Mặt khác, ta có: AD = CB = b;
∠ DAF = ∠ BCE (so le trong)
Suy ra: △ ADF = △ CBE (g.c.g)
⇒ AF = CE
Đặt AF = CE = x
Theo tính chất của đường phân giác BE trong tam giác ABC, ta có: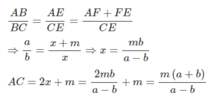
Thay số, tính trên máy tính điện tử cầm tay ta được: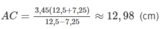
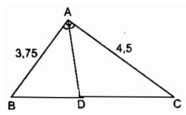
Chu vi tam giác ABC là 3 + 5 +7 = 15
Ta có :
P ABC / P A'B'C' = AB / A'B'
<=> 15 / 55 = 3 / A'B'
=> A'B' = ( 55 x 3 )/ 15 = 11 cm
P ABC / P A'B'C' = AC / A'C'
<=> 15 / 55 = 5 / A'C'
=> A'C' = ( 55 x 5 ) / 15 = 55/3 cm
P ABC / P A'B'C' = BC / B'C'
<=> 15 / 55 = 7 / B'C'
=> B'C' = ( 55 x 7 ) / 15 = 77/3 cm
\(\Rightarrow\Delta ABC\)đồng dạng \(\Delta A'B'C'\left(gt\right)\)
Áp dụng tính chất DTSBN , ta có :
\(\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}=\frac{AB+AC+BC}{A'B'+A'C'+B'C'}=\frac{C_{ABC}}{C_{A'B'C'}}\)
Hay \(\frac{3}{A'B'}=\frac{7}{B'C'}=\frac{5}{A'C'}=\frac{C_{ABC}}{55}=\frac{3+5+7}{55}=\frac{15}{55}=\frac{3}{11}\)
Với CABC và CA'B'C' lần lượt là chu vi của tam giác ABC , A'B'C'
\(+)\frac{3}{A'B'}=\frac{3}{11}\Rightarrow A'B'=\frac{3.11}{3}=11cm\)
\(+)\frac{7}{A'C'}=\frac{3}{11}\Rightarrow B'C'=\frac{7.11}{3}\approx25,67cm\)
\(+)\frac{5}{A'C'}=\frac{3}{11}\Rightarrow A'C'=\frac{5.11}{3}\approx18,33cm\)
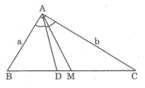
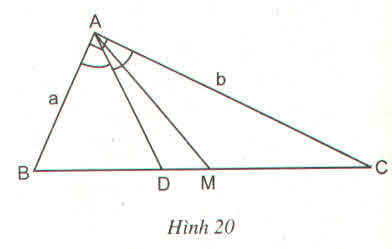
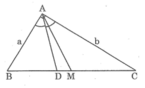
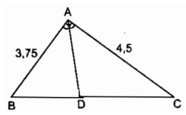
Với a = 4,15 (cm); b = 7,25 (cm), sử dụng máy tỉnh, ta tính được:
BC = 8,35 cm
BD = 3,04 cm
DC ≈ 5,31 cm
AM ≈ 4,18 cm
DM ≈ 1,14cm