Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=4.5^2+6^2=56.25\)
hay BC=7,5(cm)
Vậy: BC=7,5cm

`Answer:`
Sửa đề câu a.: Tính tỉ số diện tích hai tam giác ABD và tam giác ACD nhé.
C D H A B
a. `\triangleABD` và `\triangleACD` có chung đường cao hạ từ `A`
\(\Rightarrow\frac{S_{ABD}}{S_{ACD}}=\frac{BD}{CD}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}\)
b. Áp dụng định lý Pytago: `AB^2+AC^2=BC^2<=>12^2+16^2=BC^2<=>BC^2=400<=>BC=20cm`
c. Ta có: `BC=BD+CD=20cm`
Mà `\frac{BD}{CD}=3/4=>\frac{BD}{3}=\frac{CD}{4}=\frac{BD+CD}{3+4}=\frac{20}{7}`\(\Rightarrow\hept{\begin{cases}BD=\frac{60}{7}cm\\CD=\frac{80}{7}cm\end{cases}}\)
d. \(S_{ABC}=\frac{1}{2}.AB.AC=\frac{1}{2}.AH.BC\Rightarrow AH=\frac{12.16}{20}=9,6cm\)
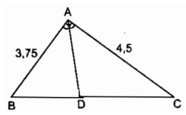
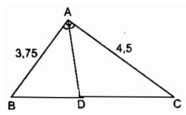

Xét tg ABC ( ^A = 90o ) có:
BC2 = AB2 + AC2 (định lý Pytago)
Thay số: BC2 = 3,752 + 4,52
BC2 = 14,0625 + 20,25
BC2 = 34,3125
BC = \(\sqrt{34,3125}\) (BC > 0)
Xét tg ABC có D là đường pg ^A ( gt )
=> \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)
<=> \(\dfrac{AB}{AC+AB}=\dfrac{BD}{CD+BD}\)
Thay số: \(\dfrac{3,75}{4,5+3,75}=\dfrac{BD}{BC}\)
<=> \(\dfrac{3,75}{8,25}=\dfrac{BD}{\sqrt{34,3125}}\)
=> BD = (cm)
=> CD = BC - CD = (cm)