NV
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QT
1
23 tháng 9 2023
Tham khảo:
Tam thức bậc hai \(f\left( x \right) = - {x^2} - 2x + 8\) có hai nghiệm phân biệt \({x_1} = - 4,{x_2} = 2\) và hệ số \(a = - 1 < 0\).
Ta có bảng xét dấu \(f\left( x \right)\) như sau:
23 tháng 9 2023
Tham khảo:
a) Ta có tam thức bậc hai \(f\left( x \right) = {x^2} - x - 2\) có 2 nghiệm phân biệt \({x_1} = - 1,{x_2} = 2\) và hệ số \(a = 1 > 0\)
Ta có bảng xét dấu f(x) như sau:
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)\)b) Từ bảng xét dấu ta thấy \(f\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}x < - 1\\x > 2\end{array} \right.\)
23 tháng 9 2023
Tham khảo:
a) \(f\left( x \right) = - 3{x^2} + 4x - 1\)
\(a = - 3 < 0\), \(\Delta = {4^2} - 4.\left( { - 3} \right).\left( { - 1} \right) = 4 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = \frac{1}{3},x = 1\)
Bảng xét dấu:
b) \(f\left( x \right) = {x^2} - x - 12\)
\(a = 1 > 0\), \(\Delta = {\left( { - 1} \right)^2} - 4.1.\left( { - 12} \right) = 49 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = - 3,x = 4\)
Bảng xét dấu:
c) \(f\left( x \right) = 16{x^2} + 24x + 9\)
\(a = 16 > 0\), \(\Delta ' = {12^2} - 16.9 = 0\)
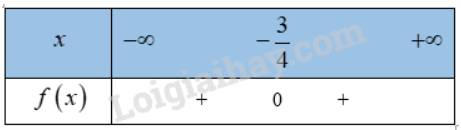
=> \(f\left( x \right)\) có nghiệm duy nhất \(x = - \frac{3}{4}\)
Bảng xét dấu:
PT
1
CM
21 tháng 6 2017
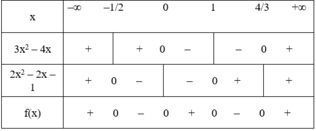
f(x) = (3x2 – 4x)(2x2 – x – 1)
+ Tam thức 3x2 – 4x có hai nghiệm x = 0 và x = 4/3, hệ số a = 3 > 0.
Do đó 3x2 – 4x mang dấu + khi x < 0 hoặc x > 4/3 và mang dấu – khi 0 < x < 4/3.
+ Tam thức 2x2 – x – 1 có hai nghiệm x = –1/2 và x = 1, hệ số a = 2 > 0
Do đó 2x2 – x – 1 mang dấu + khi x < –1/2 hoặc x > 1 và mang dấu – khi –1/2 < x < 1.
Ta có bảng xét dấu:
Kết luận:
f(x) > 0 ⇔ x ∈ (–∞; –1/2) ∪ (0; 1) ∪ (4/3; +∞)
f(x) = 0 ⇔ x ∈ {–1/2; 0; 1; 4/3}
f(x) < 0 ⇔ x ∈ (–1/2; 0) ∪ (1; 4/3)
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
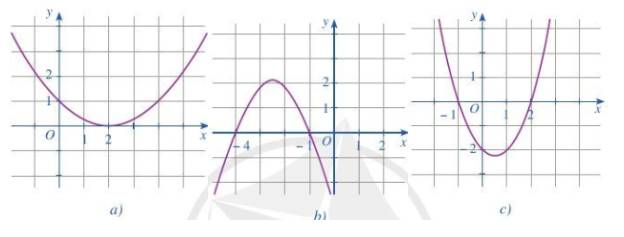
Hình 24a:
Ta thấy đồ thị cắt trục Ox tại điểm (2;0)
=> Phương trình \(f\left( x \right) = 0\) có nghiệm duy nhất \(x = 2\)
Ta thấy đồ thị nằm trên trục hoành nên có bảng xét dấu:
Hình 24b:
Ta thấy đồ thị cắt trục Ox tại 2 điểm phân biệt (-4;0) và (-1;0)
=> Phương trình \(f\left( x \right) = 0\) có 2 nghiệm phân biệt \(x = - 4,x = - 1\)
Trong các khoảng \(\left( { - \infty ; - 4} \right)\) và \(\left( { - 1; + \infty } \right)\) thì đồ thị nằm dưới trục hoành nên \(f\left( x \right) < 0\)
Trong khoảng \(\left( { - 4; - 1} \right)\) thì đồ thị nằm trên trục hoành nên \(f\left( x \right) > 0\)
Bảng xét dấu:
Hình 24c:
Ta thấy đồ thị cắt trục Ox tại 2 điểm phân biệt (-1;0) và (2;0)
=> Phương trình \(f\left( x \right) = 0\) có 2 nghiệm phân biệt \(x = - 1,x = 2\)
Trong các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {2; + \infty } \right)\) thì đồ thị nằm trên trục hoành nên \(f\left( x \right) > 0\)
Trong khoảng \(\left( { - 1;2} \right)\) thì đồ thị nằm dưới trục hoành nên \(f\left( x \right) < 0\)
Bảng xét dấu:
CM
26 tháng 10 2018
am thức f(x) = –2x2 + 3x + 5 có Δ = 9 + 40 = 49 > 0.
Tam thức có hai nghiệm phân biệt x1 = –1; x2 = 5/2, hệ số a = –2 < 0
Ta có bảng xét dấu:
Vậy f(x) > 0 khi x ∈ (–1; 5/2)
f(x) = 0 khi x = –1 ; x = 5/2
f(x) < 0 khi x ∈ (–∞; –1) ∪ (5/2; +∞)
QT
1
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
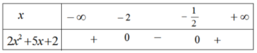
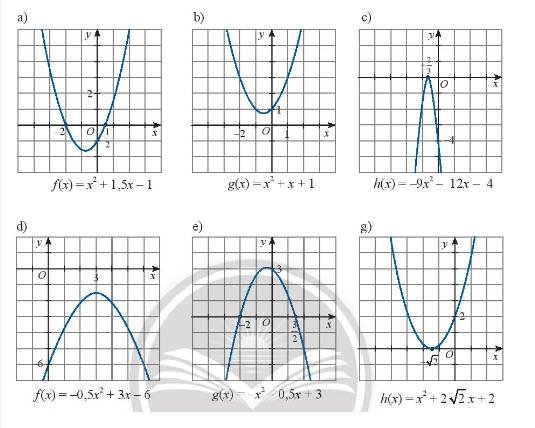
a) Tam thức \(f\left( x \right) = {x^2} + 1,5x - 1\) có hai nghiệm phân biệt \({x_1} = - 2;{x_2} = \frac{1}{2}\)
\(\)\(f\left( x \right) > 0\) khi \(x \in \left( { - \infty , - 2} \right) \cup \left( {\frac{1}{2}, + \infty } \right)\) và \(f\left( x \right) < 0\) khi \(x \in \left( { - 2,\frac{1}{2}} \right)\)
Ta có bảng xét dấu như sau
b) Tam thức \(g\left( x \right) = {x^2} + x + 1\) vô nghiệm, \(g\left( x \right) > 0\forall x \in \mathbb{R}\)
Ta có bảng xét dấu như sau
c) Tam thức \(h\left( x \right) = - 9{x^2} - 12x - 4\) có nghiệm kép \({x_1} = {x_2} = - \frac{2}{3}\) và \(h\left( x \right) < 0\forall x \ne - \frac{2}{3}\)
Ta có bảng xét dấu như sau
d) Tam thức \(f\left( x \right) = - 0,5{x^2} + 3x - 6\) vô nghiệm và \(f\left( x \right) < 0\forall x \in \mathbb{R}\)
Ta có bảng xét dấu như sau:
e) Tam thức \(g\left( x \right) = - {x^2} - 0,5x + 3\) có hai nghiệm \({x_1} = - 2,{x_2} = \frac{3}{2}\)
\(g\left( x \right) > 0\) khi \(x \in \left( { - 2,\frac{3}{2}} \right)\) và \(g\left( x \right) < 0\) khi \(x \in \left( { - \infty , - 2} \right) \cup \left( {\frac{3}{2}, + \infty } \right)\)
Ta có bảng xét dấu như
g) Tam thức \(h\left( x \right) = {x^2} + 2\sqrt 2 x + 2\) có nghiệm kép \({x_1} = {x_2} = - \sqrt 2 \)
\(h\left( x \right) > 0\forall x \ne - \sqrt 2 \)
Ta có bảng xét dấu như sau
KT
0
UK F(X) BAN G F(X)