KT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
1
17 tháng 2 2022
b: \(\Delta=2^2-4\cdot1\cdot1=0\)
Do đó: Tam thức này dương khi x khác -1; bằng 0 khi x=-1
a: \(\Delta=3^2-4\cdot\left(-5\right)\cdot\left(-1\right)=9-20=-11< 0\)
Do đó: Tam thức này luôn âm với mọi x
c: \(\Delta=1^2-4\cdot1\cdot\left(-2\right)=9\)
Do đó: Tam thức này âm khi -2<x<1
Bằng 0 khi x=-2 hoặc x=1
Dương khi x<-2 hoặc x>1
QT
1
23 tháng 9 2023
Tham khảo:
Tam thức bậc hai \(f\left( x \right) = - {x^2} - 2x + 8\) có hai nghiệm phân biệt \({x_1} = - 4,{x_2} = 2\) và hệ số \(a = - 1 < 0\).
Ta có bảng xét dấu \(f\left( x \right)\) như sau:
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) \(f\left( x \right) = 2{x^2} - 3x - 2\) có \(\Delta = 25 > 0\), hai nghiệm phân biệt là \({x_1} = - \frac{1}{2};{x_2} = 2\)
và \(a = 2 > 0\)
Ta có bảng xét dấu như sau:
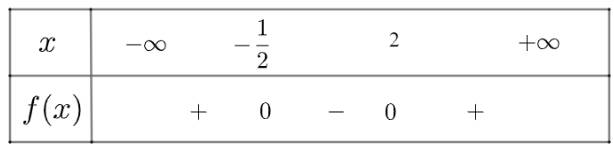
Vậy \(f\left( x \right)\) âm trong khoảng \(\left( { - \frac{1}{2},2} \right)\) và dương trong hai khoảng
\(\left( { - \infty , - \frac{1}{2}} \right)\) và \(\left( {2, + \infty } \right)\)
b) \(g\left( x \right) = - {x^2} + 2x - 3\) có \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 3} \right) = - 8 < 0\) và \(a = - 1 < 0\)
Vậy \(g\left( x \right)\)âm với mọi \(x \in \mathbb{R}\)
27 tháng 1 2022
a: \(-x^2+x+6=-\left(x-3\right)\left(x+2\right)\)
b: Đa thức này ko phân tích được nhé bạn
7 tháng 4 2017
a) F(x) = \(-x^2\left(x-1\right)\left(x+2\right)\left(x+2\right)=\left(1-x\right)x^2\left(x+2\right)^2\\ \)
\(\left\{{}\begin{matrix}x^2\ge0\\\left(x+2\right)^2\ge0\end{matrix}\right.\) => dấu biểu thức chỉ phụ thuộc vào thừa số (1-x)
F(x) =0 khi x={-2,0,1}
F(x) > 0 khi x<1 và khác -2 và 0
f(x) <0 khi x> 1
7 tháng 4 2017
Tử f(x) =x^2(x^2-3x+2) =x^2(x-1)(x-2)
tương tự a) dấu của tử phụ thuộc (x-1)(x-2)
Mẫu f(x) =x^2 -x-30 =(x-5)(x+6)
Phần hỗ trợ Lập bảng đây khó thao tác
=> viết bằng hệ {điểm tới hạn xet x={-6,0,1,2,5}
Khi => \(\left[{}\begin{matrix}x=0\\x=1\\x=2\end{matrix}\right.\)=>f(x) =0
Khi \(\left[{}\begin{matrix}x=5\\x=-6\end{matrix}\right.\) => f(x) không xác định
Khi \(x< -6\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)>0\end{matrix}\right.\)\(\Rightarrow f\left(x\right)>0\)
khi -6<x<1 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)< 0\end{matrix}\right.\) => f(x) <0
khi 1<x<2 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)< 0\\Mf\left(x\right)< 0\end{matrix}\right.\) => f(x) >0
khi 2<x<5 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)< 0\end{matrix}\right.\) => f(x) <0
khi x>5 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)>0\end{matrix}\right.\) => f(x) >0