Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Sắp sếp lại số liệu trên theo thứ tự tăng dần của điểm số

Vì n = 25 là số lẻ nên số trung vị là số đứng ở vị trí thứ 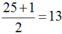
Do đó số trung vị là: Me= 75.

Chọn A.
Dựa vào bảng đã cho ta có bảng phân bố tần số; tần suất như sau:
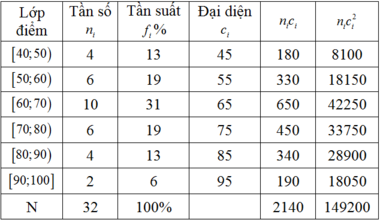
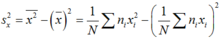
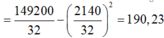

Ta lập bảng phân bố tần số ghép lớp:
Lớp |
L 1 |
L 2 |
L 3 |
L 4 |
L 5 |
L 6 |
|
Tần số |
4 |
6 |
11 |
6 |
3 |
2 |
n=32 |
Số học sinh có số điểm trong nửa khoảng [50,80) là 6+11+6=23
Chọn A

Ta lập bảng phân bố tần số- tần suất ghép lớp:
Lớp |
[40;50) | [50;60) | [60;70) | [70;80) | [80;90) | [90;100) | Cộng |
Tần số |
4 |
6 |
11 |
6 |
3 |
2 |
32 |
Tần suất (%) |
12,50 |
18,75 |
34,37 |
18,75 |
9,38 |
6,25 |
100% |
Ta thấy cột [60;70) có tần suất lớn nhất.

Chọn C.
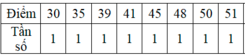
Bảng phân bố tần số:
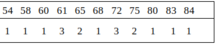
| Điểm | 30 | 35 | 39 | 41 | 45 | 48 | 50 | 51 | 54 | 58 | 60 | 61 | 65 | 68 | 72 | 75 | 80 | 83 | 87 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tần số | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 3 | 2 | 1 | 3 | 2 | 1 | 1 | 1 |
Bảng trên có 2 số có tần số lớn nhất là 61 và 72. Vậy có hai mốt là M0 = 61, M0 = 72.

a)
+) Số trung bình: \(\overline x = \frac{{23.6 + 25.8 + 28.10 + 31.6 + 33.4 + 37.3}}{{6 + 8 + 10 + 6 + 4 + 3}} \approx 28,3\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm,
\(\underbrace {23,...,23}_6,\underbrace {25,...25}_8,\underbrace {28,...,28}_{10},\underbrace {31,...,31}_6,\underbrace {33,...,33}_4,37,37,37\)
Bước 2: \(n = 6 + 8 + 10 + 6 + 4 + 3 = 37\), là số lẻ \( \Rightarrow {Q_2} = {X_{19}} = 28\)
\({Q_1}\) là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\): \(\underbrace {23,...,23}_6,\underbrace {25,...25}_8,\underbrace {28,...,28}_4\)
Do đó \({Q_1} = \frac{1}{2}({X_9} + {X_{10}}) = \frac{1}{2}(25 + 25) = 25\)
\({Q_3}\) là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\)
\(\underbrace {28,...,28}_5,\underbrace {31,...,31}_6,\underbrace {33,...,33}_4,37,37,37\)
Do đó \({Q_3} = \frac{1}{2}({X_9} + {X_{10}}) = \frac{1}{2}(31 + 31) = 31\)
+) Mốt \({M_o} = 28\)
b) Giả sử cỡ mẫu \(n = 10\)
Khi đó ta có bảng số liệu như sau:
Giá trị | 0 | 2 | 4 | 5 |
Tần số | 6 | 2 | 1 | 1 |
+) Số trung bình: \(\overline x = \frac{{0.0,6 + 2.0,2 + 4.0,1 + 5.0,1}}{{0,6 + 0,2 + 0,1 + 0,1}} = 1,3\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm \(0,0,0,0,0,0,2,2,4,5\)
Bước 2: \(n = 10\), là số chẵn \( \Rightarrow {Q_2} = \frac{1}{2}(0 + 0) = 0\)
\({Q_1}\) là trung vị của nửa số liệu: \(0,0,0,0,0\). Do đó \({Q_1} = 0\)
\({Q_3}\) là trung vị của nửa số liệu: \(0,2,2,4,5\). Do đó \({Q_3} = 2\)
+) Mốt \({M_o} = 0\)

Điểm trung bình là:
x - = 0 + 0 + 63 + . . . + 85 + 89 11 ≈ 61 , 09
Vậy điểm trung bình của các học sinh này gần với số 61 nhất.
Chọn D.

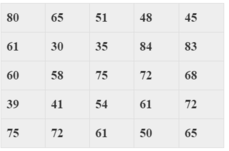
Ta có bảng phân bố tần số- tần suất ghép lớp sau:
| Lớp | [36;44) | [44;52) | [52;60) | [60;68) | [68;76) | [76;84) | Cộng |
Tần số |
3 |
6 |
6 |
8 |
3 |
4 |
30 |
Tần suất (%) |
10 |
20 |
20 |
26,7 |
10 |
13,3 |
100% |
Tần suất của L 4 lớn nhất.


Chọn D.
Ta có bảng phân bố tần số:
Bảng trên có 2 số có tần số lớn nhất là 61 và 72.
Vậy mẫu số liệu trên có hai mốt là M0= 61 và M0 = 72.