Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
Vì \(\overrightarrow{BA}\uparrow\uparrow\overrightarrow{CD}\) và \(BA=\frac{1}{3}CD\Rightarrow \overrightarrow{BA}=\frac{1}{3}\overrightarrow{CD}\)
Để $B,M,D$ thẳng hàng \(\Leftrightarrow \exists k\in\mathbb{R}|\overrightarrow{BM}=k\overrightarrow{MD}\)
\(\Leftrightarrow \overrightarrow{BA}+\overrightarrow{AM}=k\overrightarrow{MD}\)
\(\Leftrightarrow \frac{1}{3}\overrightarrow{CD}+x\overrightarrow{MC}=k\overrightarrow{MD}\)
\(\Leftrightarrow \frac{1}{3}(\overrightarrow{MC}+\overrightarrow{CD})+(x-\frac{1}{3})\overrightarrow{MC}=k\overrightarrow{MD}\)
\(\Leftrightarrow \frac{1}{3}\overrightarrow{MD}+(x-\frac{1}{3})\overrightarrow{MC}=k\overrightarrow{MD}\)
\(\Leftrightarrow (x-\frac{1}{3})\overrightarrow{MC}=(k-\frac{1}{3})\overrightarrow{MD}\)
Vì \(\overrightarrow{MC}; \overrightarrow{MD}\) không phải 2 vecto cùng phương nên điều trên chỉ xảy ra khi \(x-\frac{1}{3}=k-\frac{1}{3}=0\Rightarrow x=\frac{1}{3}\)
Bài 2:
Lấy điểm $I(a,b)$ sao cho \(\overrightarrow{IA}-2\overrightarrow{IB}+3\overrightarrow{IC}=\overrightarrow{0}\)
\(\Leftrightarrow (1-a, 1-b)-2(4-a, 3-b)+3(2-a, -2-b)=(0,0)\)
\(\Leftrightarrow (-1-2a,-11-2b)=(0,0)\Rightarrow a=-\frac{1}{2}; b=\frac{-11}{2}\)
Vậy \(I(-\frac{1}{2}; -\frac{11}{2})\)
Ta có:
\(|\overrightarrow{MA}-2\overrightarrow{MB}+3\overrightarrow{MC}|=|\overrightarrow{MI}+\overrightarrow{IA}-2(\overrightarrow{MI}+\overrightarrow{IB})+3(\overrightarrow{MI}+\overrightarrow{IC})|\)
\(|2\overrightarrow{MI}+(\overrightarrow{IA}-2\overrightarrow{IB}+3\overrightarrow{IC})|=2|\overrightarrow{MI}|\)
Để \(|\overrightarrow{MA}-2\overrightarrow{MB}+3\overrightarrow{MC}|\) min thì \(|\overrightarrow{MI}|\) min. Điều này xảy ra khi $M$ là hình chiếu của $I$ trên $Ox$
Do đó \(M=(-\frac{1}{2};0)\)

Hai đường thẳng có 2 vtpt lần lượt là \(\left(m-1;-1\right)\) và \(\left(2m;-1\right)\)
Để hai đường thẳng song song nhau
\(\Rightarrow-1\left(m-1\right)=-1.2m\Leftrightarrow m-1=2m\Rightarrow m=-1\)
Vậy đáp án B là đáp án đúng

a) ta có :
\(\Delta'=1^2-\left(-1-m\right)\left(m^2-1\right)=1-\left(-m^2+1-m^3+m\right)=1+m^2-1+m^3-m=m^3+m^2-m=m\left(m^2+m-1\right)\)để phương trình có nghiệm thì \(\Delta\ge0\)
hay \(m\left(m^2+m-1\right)\ge0\)
=> \(\left\{{}\begin{matrix}m\ge0\\m^2+m-1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2-\dfrac{5}{4}\ge0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2\ge\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left[{}\begin{matrix}m+\dfrac{1}{2}\ge\\m+\dfrac{1}{2}\le-\dfrac{\sqrt{5}}{2}\end{matrix}\right.\end{matrix}\right.\dfrac{\sqrt{5}}{2}}\)

\(a=-1< 0;\) \(-\frac{b}{2a}=1\in\left[-1;2\right]\)
\(\Rightarrow\) Hàm số đạt GTLN tại \(\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
\(y\left(-1\right)=m-7\) ; \(y\left(2\right)=m-12\)
Do \(m-7>m-12\) \(\forall m\)
\(\Rightarrow\max\limits_{\left[-1;2\right]}y=y\left(-1\right)\Rightarrow m-7=3\Rightarrow m=10\)
Đáp án D

G A B C M
A. Ta có G là trọng tâm của tam giác ABC
\(\Rightarrow\overrightarrow{AG}=2\overrightarrow{GM}\)
Hay: \(\overrightarrow{GA}=-2\overrightarrow{GM}\)
\(\Rightarrow\overrightarrow{GA}+2\overrightarrow{GM}=\overrightarrow{0}\) ( Đúng)
B. Ta có:
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OG}+\overrightarrow{GA}+\overrightarrow{OG}+\overrightarrow{GB}+\overrightarrow{OG}+\overrightarrow{GC}\)
\(=\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)+3\overrightarrow{OG}=\overrightarrow{0}+3\overrightarrow{OG}=\overrightarrow{3OG}\) ( Đúng)
C. \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\) ( Đúng, đây là điều hiển nhiên)
D. Ta có G là trọng tâm của tam giác ABC
\(\Rightarrow\overrightarrow{AM}=3\overrightarrow{GM}\)
\(\Rightarrow\overrightarrow{AM}=-3\overrightarrow{GM}\)
Vậy đáp án D sai

Lời giải:
Hàm số được coi là hàm lẻ khi mà với mọi $x\in D$ thì $-x\in D$ và $-f(x)=f(-x)$
Trong các hàm đã cho ta thấy với $y=-\frac{x}{2}$ thì:
TXĐ: $D=\mathbb{R}$.
Với mọi $x\in D$ thì $-x\in D$
$-y(x)=-(-\frac{x}{2})=\frac{x}{2}=-\frac{-x}{2}=y(-x)$
Do đó $y=\frac{-x}{2}$ là hàm lẻ. Đáp án C

a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)

Câu 1:
\(AC=\sqrt{AB^2+BC^2}=\sqrt{2}\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cos45^0=1.\sqrt{2}.\frac{\sqrt{2}}{2}=1\)
Đáp án D sai
Câu 2:
\(BN=\frac{1}{2}BM=\frac{1}{4}BC\Rightarrow4\overrightarrow{BN}=\overrightarrow{BC}\)
Ta có:
\(4\overrightarrow{AN}=4\left(\overrightarrow{AB}+\overrightarrow{BN}\right)=4\overrightarrow{AB}+4\overrightarrow{BN}=4\overrightarrow{AB}+\overrightarrow{BC}\)
\(=4\overrightarrow{AB}+\overrightarrow{BA}+\overrightarrow{AC}=4\overrightarrow{AB}-\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AB}+\overrightarrow{AC}\)
Đáp án A đúng
Chọn C.
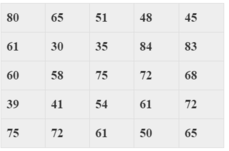
Bảng phân bố tần số:
Bảng trên có 2 số có tần số lớn nhất là 61 và 72. Vậy có hai mốt là M0 = 61, M0 = 72.