Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
= 6 : 5 : 4 : 3. Tính các góc của tứ giác ABCD.
= 600, 
= 1200, 
= 800. Tính số đo góc ngoài tại đỉnh A.
1 ta có :1 tứ giác có 4 góc và tổng phải bằng 360 độ mà 4 góc nhọn sẽ bé hơn 360(vì 1 góc nhọn <90 độ ) nên cac góc ko thể đều là góc nhọn.Đối với góc tù vẫn tương tự
2) Ta có:
\(C_{ABCD}=AB+BC+CD+AD=54\left(cm\right)\) (1)
\(C_{ABD}=AB+BD+AD=68\)
\(\Rightarrow AB=68-BD-AD\) (2)
\(C_{BCD}=BC+BD+CD=40\)
\(\Rightarrow CD=40-BC-BD\) (3)
Thay (2) và (3) vào (1) ta có:
\(68-BD-AD+BC+AD+40-BC-BD=54\)
\(\Rightarrow108-2BD=54\)
\(\Rightarrow2BD=108-54\)
\(\Rightarrow2BD=54\)
\(\Rightarrow BD=27\left(cm\right)\)
3: Nếu bốn góc trong tứ giác đều là góc nhọn thì chắc chắn tổng 4 góc cộng lại sẽ nhỏ hơn 360 độ
=>Trái với định lí tổng 4 góc trong một tứ giác
Nếu bốn góc trong tứ giác đều là góc tù thì chắc chắn tổng 4 góc cộng lại sẽ lớn hơn 360 độ
=>Trái với định lí tổng 4 góc trong một tứ giác
Do đó: 4 góc trong 1 tứ giác không thể đều là góc nhọn hay đều là góc tù được
a) + Góc ngoài tại A là góc A1:
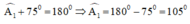
+ Góc ngoài tại B là góc B1:
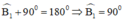
+ Góc ngoài tại C là góc C1:
+ Góc ngoài tại D là góc D1:
Theo định lý tổng các góc trong một tứ giác bằng 360º ta có:
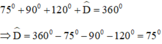
Lại có:
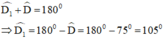
Vậy góc ngoài tại D bằng 105º.
b) Hình 7b:
Ta có:
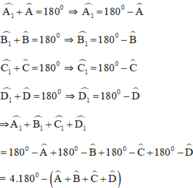
Mà theo định lý tổng bốn góc trong một tứ giác bằng 360º ta có:
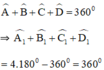
c) Nhận xét: Tổng các góc ngoài của tứ giác cũng bằng 360º.
Gỉa sử tứ giác ABCD có các góc A,B,C,D < 90.
Ta có: A+B+C+B<90+90+90+90=360
Mà tổng các góc trong 1 tứ giác bằng 360 nên một tứ giác không thể có các góc đều là góc nhọn.
Gỉa sử tứ giác ABCD có các góc A,B,C,D > 90.
Ta có: A+B+C+B>90+90+90+90=360
Mà tổng các góc trong 1 tứ giác bằng 360 nên một tứ giác không thể có các góc đều là góc tù
Giả sử cả bốn góc của tứ giác đều là góc nhọn ( tức là mỗi góc có số đo nhỏ hơn 90o) thì tổng bốn góc của tứ giác nhỏ hơn:
90 ° + 90 ° + 90 ° + 90 ° = 360 °
Vậy bốn góc của tứ giác không thể đều là góc nhọn.
Giả sử cả bốn góc của tứ giác đều là góc tù ( tức là mỗi góc có số đo lớn hơn 90 ° ) thì tổng bốn góc của tứ giác lớn hơn:
90 ° + 90 ° + 90 ° + 90 ° = 360 °
Vậy bốn góc của tứ giác không thể đều là góc tù.
Nếu các góc đều là góc nhọn: tổng các góc nhỏ hơn 360 độ => loại
Nếu các góc đều là góc tù: tổng các góc lớn hơn 360 độ => loại
Vậy...
các bạn kb vs mk nhé, mong được giúp đỡ!
Nếu các góc của tứ giác đều là góc nhọn =>Tổng 4 góc của tư giác sẽ nhỏ hơn 360 độ
Nếu các góc của tứ giác đều là góc tù=>Tổng 4 góc của tứ giác sẽ lớn hơn 360 độ
Mà tổng 4 góc tứ giác bằng 360 độ nên 4 góc của tứ giác không thể đều là góc nhọn, không thể đều là góc tù
Giả sử bốn góc của góc của tứ giác đều là góc nhọn, thế thì tổng các góc của tứ giác nhỏ hơn\(360^o\) , trái với tính chất về tổng các góc của tứ giác bằng \(360^o\)
Giả sử bốn góc của góc của tứ giác đều là góc tù, khi đó tổng các góc của tứ giác lớn hơn \(360^o\) , trái với tính chất về tổng các góc của tứ giác bằng \(360^o\)
Gỉa sử tứ giác đang xét là ABCD
Ta sẽ c/m: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}\) không thể < 90 độ
Giả sử \(\widehat{A}< 90\)o ; \(\widehat{B}< 90\)o; \(\widehat{C}< 90\)o; \(\widehat{D}< 90\)o
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}< 360\)o (vô lí)
=> Giả sử SAI
=> Các góc trong 1 tứ giác không thể đều là góc nhọn
Ta sẽ c/m: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}\)không thể > 90o
Giả sử \(\widehat{A}>90\)o ; \(\widehat{B}>90\)o ; \(\widehat{C}>90\)o ; \(\widehat{D}>90\)o
=> \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}\) > 360 độ (vô lí)
=> Giả sử SAI
=> Các góc trong 1 tứ giác không thể đều là góc tù
TH1 4 góc đều<90 độ
4 góc<360 độ(vô lí)
TH2 4 góc đều>90 độ
4 góc>360 độ(vô lí)
Vì hình tu giac co tong 4 goc la 360 độ
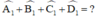
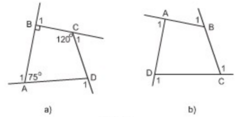
a) Tự áp dụng tính chất dãy tỉ số bằng nhau ta có :
A = 120°
B = 100°
C = 80°
D = 60°
b) Xét tứ giác ABCD có :
A + B + C + D = 360°
=> A = 360° - 60° - 120° - 80°= 100°
Góc ngoài tại A :
180° - 100° = 80°
c) Tổng quát :
Gọi góc ngoài tại A là HAD
Góc ngoài tại D là ADE
Góc ngoài tại B là CBG
Góc ngoài tại C là BCM
Ta có :
HAD = 180° - DAB
ADE = 180° ADC
CBG = 180° - ABC
BCM = 180° - BCD
=> HAD + ADE + CBG + BCM =
( 180° - DAB ) + ( 180° - ADC ) + ( 180° - ABC ) + ( 180° - BCD )
= ( 180° + 180° + 180° + 180°) - ( DAB + ACD + ABC + BCD )
= 720° - 360°
= 360°
=> Tổng các góc ngoài = 360°
d ) Nếu các góc trong tứ giác \(\le\)90°
=> Tổng 4 góc trong tứ giác đó sẽ \(\le\)360°
=> Không tồn tại tứ giác đều là góc nhọn
Nếu các góc trong tứ giác \(\ge\)90°
=> Tổng các góc trong tứ giác đó \(\ge\)360°
=> Không tồn tại tứ giác đều là góc tù