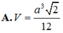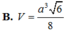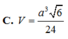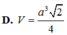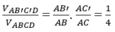Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Sử dụng các công thức diện tích tam giác ![]() và công thức Cosin
và công thức Cosin ![]()
Cách giải:
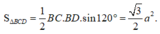
![]()
![]()
Ta có: ![]()
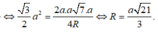
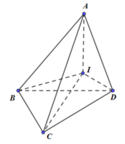
Gọi I là tâm đường tròn ngoại tiếp tam giác BCD.
Do AB = AC = AD ![]()
![]()
Thể tích tứ diện ABCD là 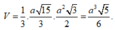
Chọn D.

Ta có O là tâm của hình hộp chữ nhật AC'BD'.A'C'B'D nên nó là tâm của mặt cầu ngoại tiếp tứ diện ABCD. Bán kính của mặt cầu ngoại tiếp tứ diện ABCD là
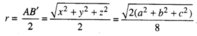
Gọi H và K theo thứ tự là chân đường vuông góc kẻ từ O đến (ABC) và (ABD). Vì OA = OB = OC nên HA = HB = HC, tương tự KA = KB = KD. Vì ΔABD = ΔBAC nên HA = KA. Do đó OH = OK. Tương tự, ta chứng minh được khoảng cách từ O đến các mặt của tứ diện ABCD bằng nhau nên O cũng là tâm của mặt cầu nội tiếp tứ diện ABCD.
Khi đó ta có V ABCD = V OABC + V OBCD + V OCDA + V ODAB
= 4 V OABC = 4 r ' S ABC / 3
Do đó:
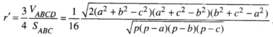
Trong đó 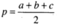

Đặt AC' = x, AD' = y, AA' = z.
Ta có:
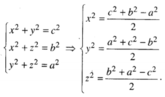
Từ đó suy ra V ABCD = V AC ' BD ' . A ' CB ' D / 3

Giải:
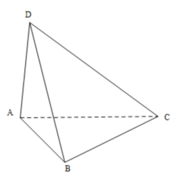
Kẻ hình chữ nhật \(ABCH\)
Dễ dàng tính được các độ dài: \(BD=\sqrt{10}a;BC=\sqrt{3}a,DC=\sqrt{7}a\)
\(\Rightarrow DC\perp BC\)
Ta có \(\left\{\begin{matrix} AH\perp AB\\ DA\perp AB\end{matrix}\right.\Rightarrow AB\perp (ADH)\rightarrow AB\perp DH\)
Tương tự do \(DC\perp BC,BC\perp HC\) nên \(DH\perp BC\)
\(\Rightarrow DH\perp (ABCH)\)
Theo hệ thức Pitago: \(DH=\sqrt{AD^2-AH^2}=\sqrt{6}a\)
Do đó thể tích \(ABCD\) là : \(V=\frac{S_{ABC}.DH}{3}=\frac{AB.BC.DH}{6}=\frac{\sqrt{2}a^3}{2}\)

Đáp án: A.
§ Hướng dẫn giải:
Dễ dàng ta có được
V A B ' C ' D V A B C D = A B ' A B . A C ' A C = 1 4