Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Xét phép thử: “Chọn ngẫu nhiên ba số từ tập S = {1;2;3;4;5;6;7;8;9}. Ta có ![]() .
.
Gọi A là biến cố: “trong ba số được chọn ra không chứa hai số nguyên liên tiếp”.
Gọi
a
1
,
a
2
,
a
3
là ba số thỏa mãn ![]() .
.
Không có hai số nguyên liên tiếp nào ![]() .
.
Đặt ![]() . Khi đó:
. Khi đó: ![]() .
.
Số cách chọn bộ ba số ![]() => có
C
7
3
cách chọn
a
1
,
a
2
,
a
3
=> có
C
7
3
cách chọn
a
1
,
a
2
,
a
3
Suy ra ![]()
Do đó 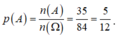

a. Không gian mẫu: \(C_{10}^3\)
Số cách chọn 3 số nguyên liên tiếp: 8 cách (123; 234;...;8910)
Số cách chọn ra 3 số trong đó có đúng 2 số nguyên liên tiếp:
- Cặp liên tiếp là 12 hoặc 910 (2 cách): số còn lại có 7 cách chọn
- Cặp liên tiếp là 1 trong 7 cặp còn lại: số còn lại có 6 cách chọn
Vậy có: \(C_{10}^3-\left(8+2.7+7.6\right)=56\) bộ thỏa mãn
Xác suất: \(P=\dfrac{56}{C_{10}^3}=...\)
b.
Có 2 số chia hết cho 4 là 4 và 8
Rút ra k thẻ: \(C_{10}^k\) cách
Số cách để trong k thẻ có ít nhất 1 thẻ chia hết cho 4: \(C_{10}^k-C_8^k\)
Xác suất thỏa mãn: \(P=\dfrac{C_{10}^k-C_8^k}{C_{10}^k}>\dfrac{13}{15}\)
\(\Leftrightarrow\dfrac{2}{15}>\dfrac{C_8^k}{C_{10}^k}=\dfrac{\dfrac{8!}{k!\left(8-k\right)!}}{\dfrac{10!}{k!\left(10-k\right)!}}=\dfrac{\left(9-k\right)\left(10-k\right)}{90}\)
\(\Leftrightarrow\left(9-k\right)\left(10-k\right)-12< 0\Leftrightarrow k^2-19k+78< 0\)
\(\Rightarrow6< k< 13\)

Ta có thể sử dụng phương pháp đếm để giải quyết bài toán này.
Để 3 số được chọn không có hai số liên tiếp nhau, ta có thể chọn 3 số bất kỳ và đặt khoảng cách giữa chúng là 1, có nghĩa là không có số nào ở giữa. Khoảng cách này có thể nằm ở bất kỳ vị trí nào trong 17 khoảng cách của tập hợp A (có thể thấy rằng tập A có tổng cộng 20 - 2 = 18 khoảng cách giữa các số).
Vậy ta có tổng cộng 17 cách chọn 3 số không có hai số liên tiếp nhau. Số trường hợp chọn 3 số trong tổng số 20 số là C(20,3) = 1140.
Vậy xác suất cần tìm là: P = 17/1140 = 0.0149 (làm tròn đến 4 chữ số thập phân).
Vậy đáp án là 0.0149.

Câu 1:
Gọi số tổng quát là \(X=\overline{ab}\)
a có 9 cách chọn
b có9 cách chọn
=>Có 9*9=81(số)
Số cách chọn ngẫu nhiên 3 số từ tập A là \(C^3_{81}\left(cách\right)\)
Câu 2:
\(\overline{abc}\)
a có 9 cách
b có 9 cách
c có 8 cách
=>có 9*9*8=81*8=648(số)
Số cách chọn ngẫu nhiên 2 số từ tập A là \(C^2_{648}\left(cách\right)\)
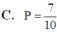


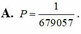
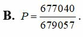
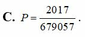
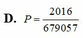



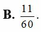
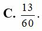
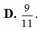



Đáp án D
Chon 3 số bất kì có C 10 3 = 120 cách
TH1: 3 số chọn ra là 3 số tự nhiên liên tiếp có 8 cách
TH2: 3 số chọn ra là 2 số tự nhiên liên tiếp
+) 3 số chọn ra có cặp (1;2) hoặc (9;10) có 2.7 = 14 cách
+) 3 số chọn ra có cặp ( 2 ; 3 ) ; ( 3 ; 4 ) ; . . . . ( 8 ; 9 ) có 6.6 = 36 cách
Vậy xác suất cần tìm là