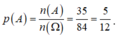Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Chon 3 số bất kì có C 10 3 = 120 cách
TH1: 3 số chọn ra là 3 số tự nhiên liên tiếp có 8 cách
TH2: 3 số chọn ra là 2 số tự nhiên liên tiếp
+) 3 số chọn ra có cặp (1;2) hoặc (9;10) có 2.7 = 14 cách
+) 3 số chọn ra có cặp ( 2 ; 3 ) ; ( 3 ; 4 ) ; . . . . ( 8 ; 9 ) có 6.6 = 36 cách
Vậy xác suất cần tìm là
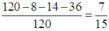

Chọn A
+ Ta có ![]()
![]()
Ta có d có 4 cách chọn {2;4;6;8}, a có 9 cách chọn, b có 9 cách chọn. Vì a + b + d khi chia cho 3 có 3 khả năng số dư
{0;1;2}, mà ![]() nên c có 3 cách chọn.
nên c có 3 cách chọn.
Ta có: ![]()
Xác suất cần tìm là: 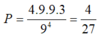

n(S)=6!
Để thỏa mãn yêu cầu đề bài thì cần chọn ra 3 số có tổng là 12
=>Số trường hợp thỏa mãn là (1;5;6); (2;4;6); (3;4;5)
=>Có 3*3!*3!
=>P=3/20

Chọn B
Số phần tử của không gian mẫu ![]()
Gọi biến cố A” Chọn được một số thỏa mãn ![]() ”.
”.
Vì mà nên trong các chữ số sẽ không có số 0.
TH1: Số được chọn có chữ số giống nhau có 9 số.
TH2: Số được chọn tạo bới hai chữ số khác nhau.
Số cách chọn ra 2 chữ số khác nhau từ 9 chữ số trên là: C 9 2 .
Mỗi bộ 2 chữ số được chọn tạo ra 2 số thỏa mãn yêu cầu.
Vậy có 2. C 9 2 số thỏa mãn.
TH3: Số được chọn tạo bởi ba chữ số khác nhau.
Số cách chọn ra 3 chữ số khác nhau từ 9 chữ số trên là: C 9 3 .
Mỗi bộ 3 chữ số được chọn chỉ tạo ra một số thỏa mãn yêu cầu.
Vậy có C 9 3 số thỏa mãn.
Vậy ![]()
Xác suất của biến cố A là: .
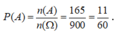

Ta có thể sử dụng phương pháp đếm để giải quyết bài toán này.
Để 3 số được chọn không có hai số liên tiếp nhau, ta có thể chọn 3 số bất kỳ và đặt khoảng cách giữa chúng là 1, có nghĩa là không có số nào ở giữa. Khoảng cách này có thể nằm ở bất kỳ vị trí nào trong 17 khoảng cách của tập hợp A (có thể thấy rằng tập A có tổng cộng 20 - 2 = 18 khoảng cách giữa các số).
Vậy ta có tổng cộng 17 cách chọn 3 số không có hai số liên tiếp nhau. Số trường hợp chọn 3 số trong tổng số 20 số là C(20,3) = 1140.
Vậy xác suất cần tìm là: P = 17/1140 = 0.0149 (làm tròn đến 4 chữ số thập phân).
Vậy đáp án là 0.0149.
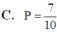
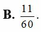
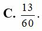
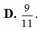



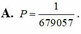
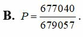
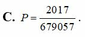
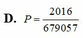


Chọn D
Xét phép thử: “Chọn ngẫu nhiên ba số từ tập S = {1;2;3;4;5;6;7;8;9}. Ta có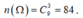 .
.
Gọi A là biến cố: “trong ba số được chọn ra không chứa hai số nguyên liên tiếp”.
Gọi a 1 , a 2 , a 3 là ba số thỏa mãn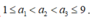 .
.
Không có hai số nguyên liên tiếp nào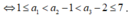 .
.
Đặt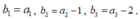 . Khi đó:
. Khi đó: 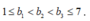 .
.
Số cách chọn bộ ba số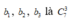 => có
C
7
3
cách chọn
a
1
,
a
2
,
a
3
=> có
C
7
3
cách chọn
a
1
,
a
2
,
a
3
Suy ra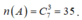
Do đó