Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Có 900 số tự nhiên có 3 chữ số \( \Rightarrow n\left( \Omega \right) = 900\)
Gọi \({A_1}\) là biến cố: “Số được chọn chia hết cho 2”, \({A_2}\) là biến cố “Số được chọn chia hết cho 7”.
Vậy \({A_1}{A_2}\) là biến cố “Số được chọn chia hết cho 14”, \(A = {A_1} \cup {A_2}\) là biến cố “Số được chọn chia hết cho 2 hoặc 7”.
Có 450 số có 3 chữ số chia hết cho 2 \( \Rightarrow n\left( {{A_1}} \right) = 450 \Rightarrow P\left( {{A_1}} \right) = \frac{{n\left( {{A_1}} \right)}}{{n\left( \Xi \right)}} = \frac{{450}}{{900}} = \frac{1}{2}\)
Có 128 số có 3 chữ số chia hết cho 7 \( \Rightarrow n\left( {{A_2}} \right) = 128 \Rightarrow P\left( {{A_2}} \right) = \frac{{n\left( {{A_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{128}}{{900}} = \frac{{32}}{{225}}\)
Có 64 số có 3 chữ số chia hết cho 14
\( \Rightarrow n\left( {{A_1}{A_2}} \right) = 64 \Rightarrow P\left( {{A_1}{A_2}} \right) = \frac{{n\left( {{A_1}{A_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{64}}{{900}} = \frac{{16}}{{225}}\)
\( \Rightarrow P\left( A \right) = P\left( {{A_1} \cup {A_2}} \right) = P\left( {{A_1}} \right) + P\left( {{A_2}} \right) - P\left( {{A_1}{A_2}} \right) = \frac{1}{2} + \frac{{32}}{{225}} - \frac{{16}}{{225}} = \frac{{257}}{{450}}\)
Gọi \({B_1}\) là biến cố: “Số được chọn có 3 chữ số chẵn”, \({B_2}\) là biến cố “Số được chọn có 1 chữ số chẵn và 2 chữ số lẻ”.
Vậy \(B = {B_1} \cup {B_2}\) là biến cố “Số được chọn có tổng các chữ số là số chẵn”.
Có \(4.5.5 = 100\) số có 3 chữ số chẵn \( \Rightarrow n\left( {{B_1}} \right) = 100 \Rightarrow P\left( {{B_1}} \right) = \frac{{n\left( {{B_1}} \right)}}{{n\left( \Omega \right)}} = \frac{{100}}{{900}} = \frac{1}{9}\)
Có \(4.5.5 = 100\) số có 3 chữ số có chữ số hàng trăm chẵn, 2 chữ số còn lại lẻ.
Có \(5.5.5 = 125\) số có 3 chữ số có chữ số hàng chục chẵn, 2 chữ số còn lại lẻ.
Có \(5.5.5 = 125\) số có 3 chữ số có chữ số hàng đơn vị chẵn, 2 chữ số còn lại lẻ.
\( \Rightarrow n\left( {{B_2}} \right) = 100 + 125 + 125 = 350 \Rightarrow P\left( {{B_2}} \right) = \frac{{n\left( {{B_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{350}}{{900}} = \frac{7}{{18}}\)
Vì \({B_1}\) và \({B_2}\) là hai biến cố xung khắc nên ta có:
\(P\left( B \right) = P\left( {{B_1} \cup {B_2}} \right) = P\left( {{B_1}} \right) + P\left( {{B_2}} \right) = \frac{1}{9} + \frac{7}{{18}} = \frac{1}{2}\)
Đáp án B.
Số phần tử của E là 
.
Từ 5 chữ số đã cho ta có 4 bộ gồm 3 chữ số có tổng chia hết cho 3 là 
. Mỗi bộ 3 chữ số này ta lập được 
số thuộc tập hợp E. Vậy trong tập hợp E có 
số chia hết cho 3.
Gọi A là biến cố “Số được chọn từ E chia hết cho 3” thì 
.
Vậy xác suất cần tính là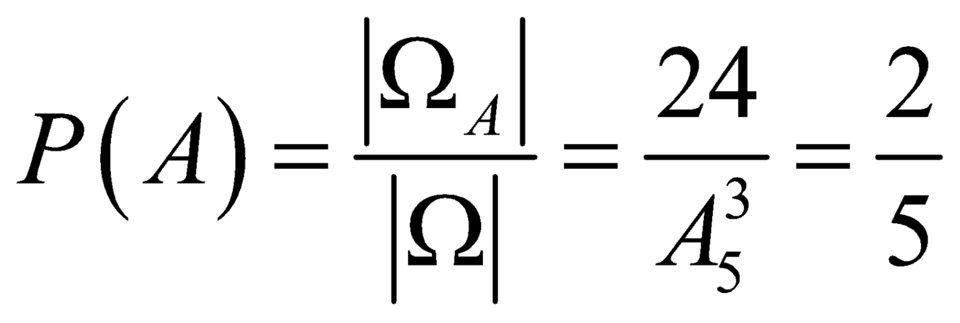 
.
Đáp án D
Chon 3 số bất kì có C 10 3 = 120 cách
TH1: 3 số chọn ra là 3 số tự nhiên liên tiếp có 8 cách
TH2: 3 số chọn ra là 2 số tự nhiên liên tiếp
+) 3 số chọn ra có cặp (1;2) hoặc (9;10) có 2.7 = 14 cách
+) 3 số chọn ra có cặp ( 2 ; 3 ) ; ( 3 ; 4 ) ; . . . . ( 8 ; 9 ) có 6.6 = 36 cách
Vậy xác suất cần tìm là
.
