Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nhé.
a.
Xét tứ giác AEBD có:
AH = HB (H là trung điểm của AB)
HE = HD (vì E và D đối xứng với nhau qua H)
=> AEBD là hình bình hành.
Lại có: \(\widehat{ADB}=90^o\) (AD là đường trung tuyến của tam giác cân ABC)
Từ trên suy ra: AEBD là hình chữ nhật.
b.
Vì AEBD là hình chữ nhật nên ta có:
- AE // BD và AE = BD (1)
mà: BC // AE và BD = DC (2)
Từ (1), (2) suy ra: ACDE là hình bình hành.
c.
có: \(S_{AEBD}=AD.DB=\dfrac{1}{2}.AD.BC=S_{ABC}\)
d.
Để AEBD là hình vuông thì AD = BD
=> \(AD=\dfrac{1}{2}BC\) => Tg ABC vuông.
Mà AB = AC
=> Điều kiện của tam giác ABC là vuông cân tại A để AEBD là hình vuông.

a) Xét tam giác ABC cân tại A: AD là phân giác (gt).
\(\Rightarrow\) AD là đường cao (Tính chất các đường trong tam giác cân).
\(\Rightarrow\) AD \(\perp\) BC.
Xét tứ giác AEBD có:
\(+\) I là trung điểm của AB (gt).
\(+\) I là trung điểm của ED (E là điểm đối xứng với D qua I).
\(\Rightarrow\) Tứ giác AEBD là hình bình hành (dhnb).
Mà \(\widehat{ADB}\) = 90o (AD \(\perp\) BC).
\(\Rightarrow\) Tứ giác AEBD là hình chữ nhật (dhnb).
b) Xét tam giác ABC cân tại A: AD là phân giác (gt).
\(\Rightarrow\) AD là trung tuyến (Tính chất các đường trong tam giác cân).
\(\Rightarrow\) D là trung điểm của BC. \(\Rightarrow\) BD = DC.
Mà BD = EA (Tứ giác AEBD là hình chữ nhật).
\(\Rightarrow\) EA = DC (= BD).
Tứ giác AEBD là hình chữ nhật (cmt).
\(\Rightarrow\) EA // DC (Tính chất hình chữ nhật).
Xét tứ giác AEDC có:
\(+\) EA = DC (cmt).
\(+\) EA // DC (EA // BD).
\(\Rightarrow\) Tứ giác AEDC là hình bình hành (dhnb).

Giải:
a) Ta có AM=MB và EM=MD ( đối xứng ) =>AEBD là hình bình hành
mà góc D = 90 (độ) => AEBD là hình chữ nhật
b) từ câu a =>AE//DC ; mà DC=DB (AD là đường cao của tam giác cân ABC =>là AD cũng đường trung tuyến)
=>ACDE là hình bình hành
c) để tứ giác AEBD là hình vuông thì:
như câu a thì AEBD là hình chữ nhật =>điều hiện là:AD=BD mà AD=BD =>tam giác ABC phải là tam giác vuông cân
d) S tam giác ABC= AD.BD/2 = AD.BD 1
S hình chữ nhật ABDE= AD.BD 2
Từ 1 và 2 =>S tam giác ABC = S hình chữ nhật ABDE (đpcm)

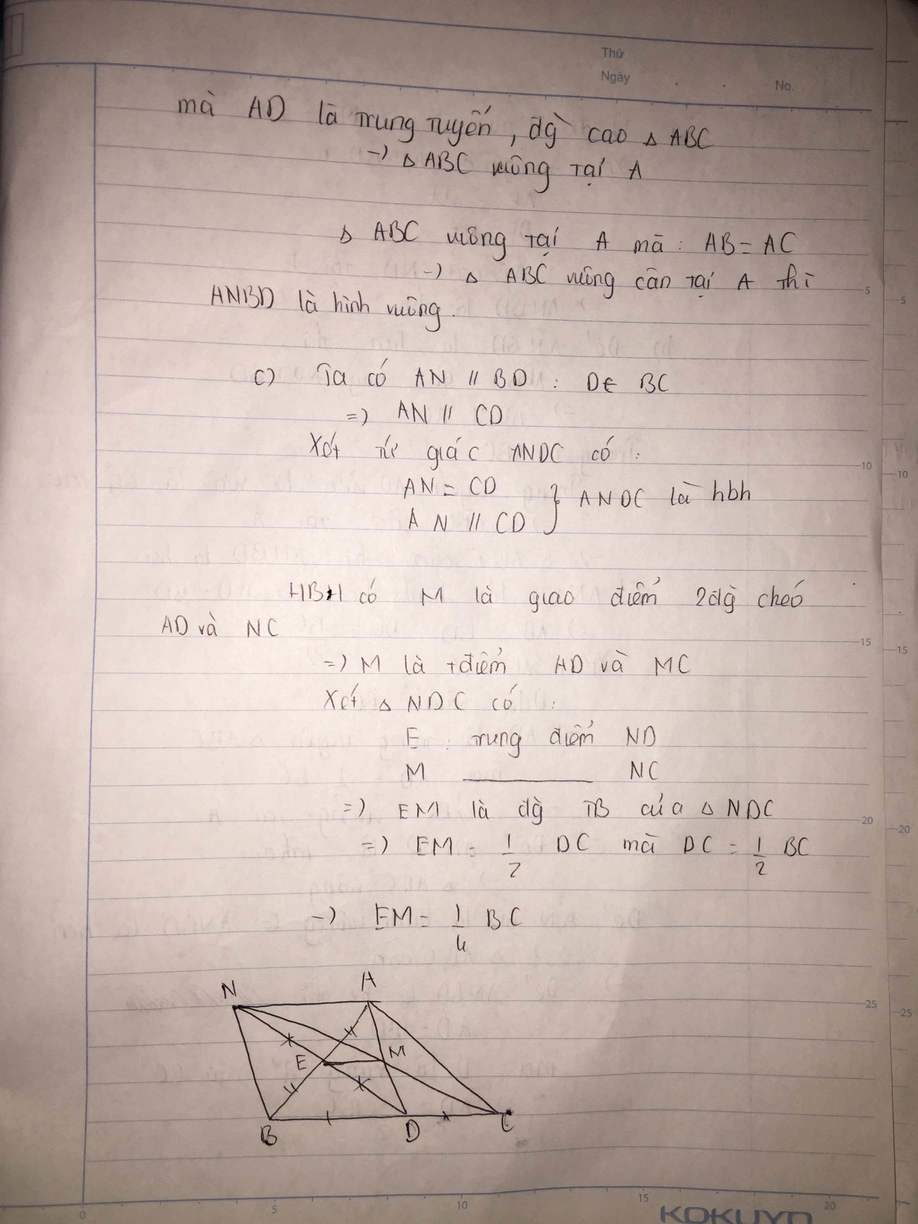
a/ Ta có MD là đường tb tam giác BAC nên ME//AC(1)
Mà vì \(\Delta AEM=\Delta BDM\left(c.g.c\right)\Rightarrow\widehat{AEM}=\widehat{BDM}\Rightarrow\)AE//BC(2)
Từ (1) và (2) suy ra ngay ĐPCM
b/ Từ giả thiết là D,E và A,B đối xứng với nhau qua điểm M suy ra AEBD là hbh
Từ đó để AEBD là hình chữ nhật thì MD phải vuông góc với BC Từ đó suy ra tam giác ACB phải vuông ở C
6ytt