Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 3 :
\(1,\left\{{}\begin{matrix}\dfrac{3}{\sqrt{y-2}}+x-2y=5\\\dfrac{1}{\sqrt{y-2}}-2x+4y=4\end{matrix}\right.\) \(\left(ĐK:y>2\right)\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{\sqrt{y-2}}+x-2y=5\\\dfrac{1}{\sqrt{y-2}}-2\left(x-2y\right)=4\end{matrix}\right.\) Đặt : \(\left\{{}\begin{matrix}a=\dfrac{1}{\sqrt{y-2}}\\b=x-2y\end{matrix}\right.\)
Ta có Hpt trở thành : \(\left\{{}\begin{matrix}3a+b=5\\a-2b=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=-1\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{\sqrt{y-2}}=2\\x-2y=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{y-2}=1\\x-2y=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{5}{4}\\x-2.\dfrac{5}{4}=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{5}{4}\end{matrix}\right.\)
Vậy ....
\(2,x^2-\left(2m+1\right)+m^2-m+1=0\left(1\right)\)
a, Thay m = 2 vào pt (1) có : \(x^2-5x+3=0\)
\(\Delta=5^2-4.3=13>0\Rightarrow\sqrt{\Delta}=\sqrt{13}\)
⇒ Phương trình có hai nghiệm phân biệt
\(x_1=\dfrac{5+\sqrt{13}}{2};x_2=\dfrac{5-\sqrt{13}}{2}\)
Vậy \(S=\left\{\dfrac{5\pm\sqrt{13}}{2}\right\}\) khi \(m=2\)
b, Để phương trình có hai nghiệm phân biệt thì \(\Delta>0\)
\(\Rightarrow\left(2m+1\right)^2-4m^2+4m-4>0\Leftrightarrow4m^2+4m+1-4m^2+4m-4>0\Leftrightarrow8m-3>0\Leftrightarrow m>\dfrac{3}{8}\)
Vậy...
2:
Gọi số cần tìm là \(\overline{ab}\)
Theo đề, ta có: a-b=3 và a^2+b^2=45
=>a=b+3 và (b+3)^2+b^2=45
=>b=3
=>a=6

Câu 2:
\(C=-x+\sqrt{x}\)
\(=-\left(x-\sqrt{x}+\dfrac{1}{4}\right)+\dfrac{1}{4}\)
\(=-\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{4}\)

Câu 17 :
- Ta có : AD là đường phân giác của tam giác ABC .\(\Rightarrow\dfrac{AB}{BD}=\dfrac{AC}{CD}\)
- Áp dụng tính chất dãy tỉ số bằng nhau :\(\dfrac{AB}{BD}=\dfrac{AC}{CD}=\dfrac{12}{BD}=\dfrac{16}{CD}\)
\(=\dfrac{12+16}{BD+CD}=\dfrac{28}{14}=2=\dfrac{16-12}{CD-BD}\)
\(\Rightarrow CD-BD=\dfrac{4}{2}=2\)
- Đáp án C.
Câu 16 :
- Ta có : \(\widehat{COB}=2\widehat{BAC}=120^o\)
- Ta lại có : \(S=S_{\stackrel\frown{BC}}-S_{OBC}=\dfrac{\pi R^2.120}{360}-\dfrac{1}{2}R.R.Sin120=\dfrac{\pi R^2}{3}-\dfrac{R^2\sqrt{3}}{4}\)
\(=\dfrac{R^2\left(4\pi-3\sqrt{3}\right)}{12}\) ( đvdt )
Đáp án D

Bài 4:
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
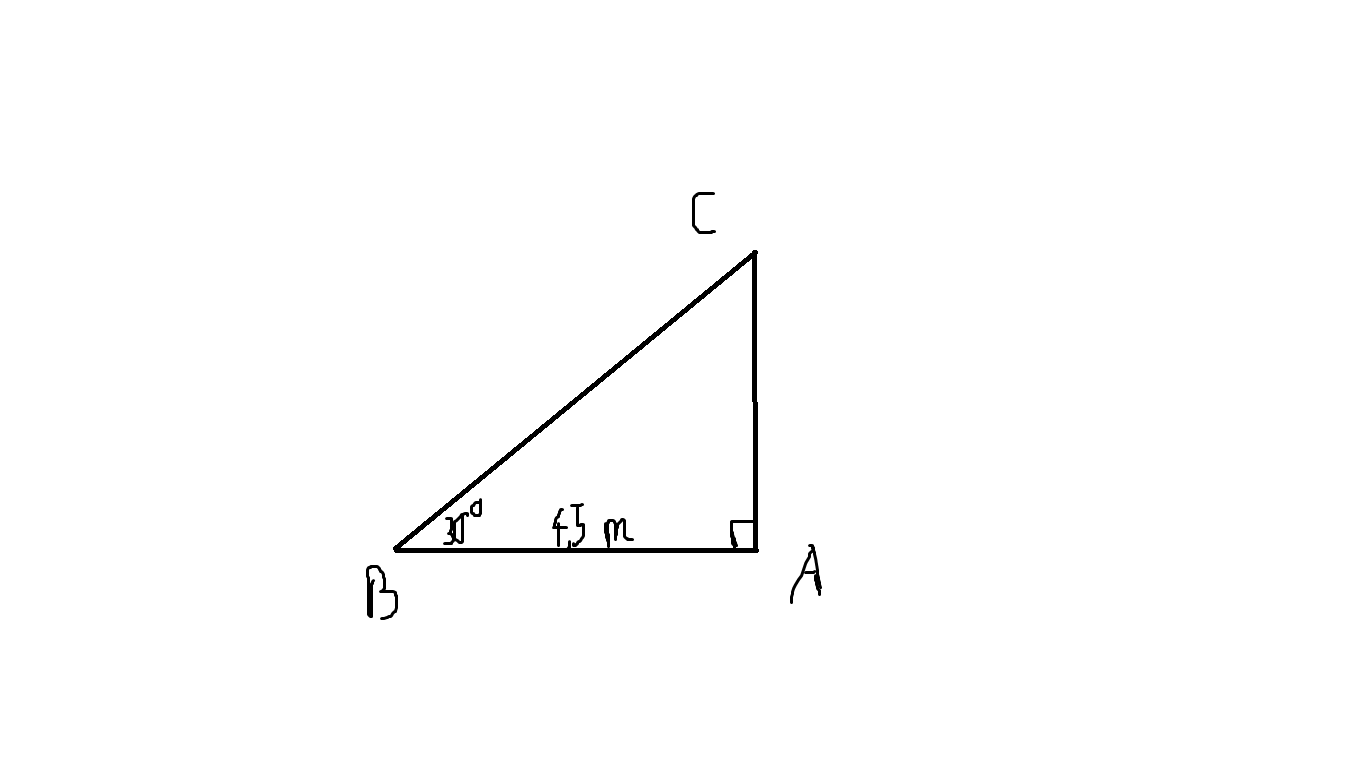
\(TanB=\dfrac{AC}{AB}\Rightarrow Tan30^o=\dfrac{AC}{4,5}\Rightarrow AC=Tan30^o.4,5=\dfrac{3\sqrt{3}}{2}\left(m\right)\)
\(CosB=\dfrac{AB}{BC}\Rightarrow Cos30^o=\dfrac{4,5}{BC}\Rightarrow BC=Cos30^o.4,5=\dfrac{9\sqrt{3}}{4}\)
Chiều cao ban đầu của cây tre là: \(\dfrac{3\sqrt{3}}{2}+\dfrac{9\sqrt{3}}{4}=\dfrac{15\sqrt{3}}{4}\approx6,5\left(m\right)\)