CG
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 2 2022
a/ Khi \(m=5\Leftrightarrow\left(d\right):y=6x-5\)
Phương trình hoành độ giao điểm của \(\left(d\right);\left(P\right)\) là :
\(x^2=6x-5\)
\(\Leftrightarrow x^2-6x+5=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}M\left(5;25\right)\\N\left(1,1\right)\end{matrix}\right.\) là giao điểm của \(\left(P\right)\) và \(\left(d\right)\) khi \(m=5\)
b/ Phương trình hoành độ giao điểm của \(\left(P\right);\left(d\right)\) là :
\(x^2=\left(m+1\right)x-m\)
\(\Leftrightarrow x^2-\left(m+1\right)+m=0\)
\(\Delta=\left(m+1\right)^2-4m=m^2-2m+1=\left(m+1\right)^2\ge0\)
Để pt có 2 nghiệm pb \(\Leftrightarrow m\ne-1\)
Ta có :
\(y_1-y_2=4\)
\(\Leftrightarrow x_1^2-x_2^2=4\)
\(\Leftrightarrow\left(x_1+x_2\right)\left(x_1-x_2\right)=4\)
Theo định lí Viet ta có :
\(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1.x_2=m\end{matrix}\right.\)
\(\Leftrightarrow x_1-x_2=\dfrac{4}{m+1}\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=\dfrac{16}{\left(m+1\right)^2}\)
\(\Leftrightarrow x_1^2+x_2^2-2x_1.x_2=\dfrac{16}{\left(m+1\right)^2}\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1.x_2=\dfrac{16}{\left(m+1\right)^2}\)
\(\Leftrightarrow\left(m+1\right)^2-4m=\dfrac{16}{\left(m+1\right)^2}\)
\(\Leftrightarrow\left(m-1\right)^2.\left(m+1\right)^2=16\)
\(\Leftrightarrow\left(m^2-1\right)^2=16\)
\(\Leftrightarrow m^2-1=\pm4\)
\(\Leftrightarrow\left[{}\begin{matrix}m^2=3\\m^2=-3\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow m=\pm\sqrt{3}\)
Vậy..
15 tháng 1
Bài 2:
gọi thời gian chảy riêng từng vòi đầy bể lần lượt là x(giờ) và y(giờ)
(Điều kiện: x>0 và y>0)
Trong 1h, vòi thứ nhất chảy được \(\dfrac{1}{x}\left(bể\right)\)
Trong 1h, vòi thứ hai chảy được \(\dfrac{1}{y}\left(bể\right)\)
TRong 1h, hai vòi chảy được \(\dfrac{1}{4}\left(bể\right)\)
=>\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\left(1\right)\)
Trong 10h, vòi thứ nhất chảy được \(\dfrac{10}{x}\left(bể\right)\)
Nếu mở vòi thứ nhất chảy trong 10 giờ rồi khóa lại và mở vòi thứ hai chảy trong 1 giờ nữa thì đầy bể nên ta có:
\(\dfrac{10}{x}+\dfrac{1}{y}=1\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\\\dfrac{10}{x}+\dfrac{1}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{9}{x}=-\dfrac{3}{4}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=12\\\dfrac{1}{y}=\dfrac{1}{4}-\dfrac{1}{12}=\dfrac{3}{12}-\dfrac{1}{12}=\dfrac{2}{12}=\dfrac{1}{6}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=12\\y=6\end{matrix}\right.\left(nhận\right)\)
Vậy: Thời gian để vòi một chảy một mình đầy bể là 12 giờ
Thời gian để vòi thứ hai chảy một mình đầy bể là 6 giờ
T
3
22 tháng 6 2023
a: \(C=\dfrac{x+\sqrt{x}-x+\sqrt{x}}{x-1}\cdot\dfrac{\sqrt{x}-1}{\sqrt{x}}=\dfrac{2}{\sqrt{x}+1}\)
b: C<1
=>\(\dfrac{2-\sqrt{x}-1}{\sqrt{x}+1}< 0\)
=>1-căn x<0
=>x>1
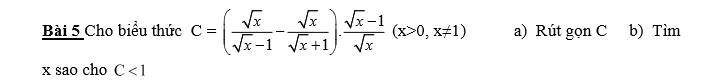
giúp tui bài 1 với :3