
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2:
a: \(A=\dfrac{x_1+x_2}{x_1x_2}=\dfrac{-6}{3}=-2\)
b: \(B=\dfrac{\left(x_1+x_2\right)^2-3x_1x_2}{1-x_1x_2}=\dfrac{36-3\cdot3}{1-3}=\dfrac{36-9}{-2}=-\dfrac{27}{2}\)
c: \(C=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)
\(=\sqrt{\left(-6\right)^2-4\cdot3}=2\sqrt{6}\)
d: \(D=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)-3x_1x_2\)
\(=\left(-6\right)^3-3\cdot3\cdot\left(-6\right)-3\cdot3\)
=261

a: \(\left\{{}\begin{matrix}3x-2y=4\\2x+y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-2y=4\\4x+2y=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7x=14\\2x+y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=5-2x=5-2\cdot2=1\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}-x+2y=2\\2x-y=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2x+4y=4\\2x-y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3y=3\\x-2y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=1\\x=-2+2y=-2+2\cdot1=0\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}2x-y=13\\y-5=-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-y=13\\y=-7+5=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=y+13=-2+13=11\\y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{11}{2}\\y=-2\end{matrix}\right.\)
d: \(\left\{{}\begin{matrix}3x+y=8\\2x-3y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x+3y=24\\2x-3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=25\\3x+y=8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{25}{11}\\y=8-3x=8-3\cdot\dfrac{25}{11}=8-\dfrac{75}{11}=\dfrac{13}{11}\end{matrix}\right.\)

\(Q=\left(\dfrac{1}{2\sqrt{x}+1}+\dfrac{1}{2\sqrt{x}-1}\right):\dfrac{1}{1-4x}\)
\(=\left(\dfrac{2\sqrt{x}-1}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}+\dfrac{2\sqrt{x}+1}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}\right).\left(1-4x\right)\)
\(=\left(\dfrac{2\sqrt{x}-1+2\sqrt{x}+1}{4x-1}\right)\left(1-4x\right)\)
\(=\dfrac{-4\sqrt{x}.\left(4x-1\right)}{4x-1}=-4\sqrt{x}\)
\(Q=\left(\dfrac{1}{2\sqrt{x}+1}+\dfrac{1}{2\sqrt{x}-1}\right):\dfrac{1}{1-4x}\left(dkxd:x\ge0;x\ne\dfrac{1}{4}\right)\)
\(=\left[\dfrac{2\sqrt{x}-1}{\left(2\sqrt{x}-1\right)\left(2\sqrt{x}+1\right)}+\dfrac{2\sqrt{x}+1}{\left(2\sqrt{x}-1\right)\left(2\sqrt{x}+1\right)}\right]\cdot\left(1-4x\right)\)
\(=\dfrac{2\sqrt{x}-1+2\sqrt{x}+1}{4x-1}\cdot\left[-\left(4x-1\right)\right]\)
\(=4\sqrt{x}\cdot\left(-1\right)\)
\(=-4\sqrt{x}\)

a: \(C=\dfrac{x+\sqrt{x}-x+\sqrt{x}}{x-1}\cdot\dfrac{\sqrt{x}-1}{\sqrt{x}}=\dfrac{2}{\sqrt{x}+1}\)
b: C<1
=>\(\dfrac{2-\sqrt{x}-1}{\sqrt{x}+1}< 0\)
=>1-căn x<0
=>x>1

\(\left\{{}\begin{matrix}x+2y=2\left(1\right)\\-2x+y=1\left(2\right)\end{matrix}\right.\)
Từ (2) ta có \(y=2x+1\) (3)
Thế vào (1) \(\Rightarrow x+2\left(2x+1\right)=2\)
\(\Leftrightarrow5x=0\)
\(\Rightarrow x=0\)
Thế \(x=0\) vào (3) ta được \(y=1\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(0;1\right)\)

Bài 6
a, bạn tự vẽ
b, Hoành độ giao điểm (P) ; (d) tm pt
\(\dfrac{1}{4}x^2+mx-2m-1=0\Leftrightarrow x^2+4mx-8m-4=0\)
\(\Delta'=4m^2-\left(-8m-4\right)=4m^2+8m+4=4\left(m+1\right)^2\)
Để (P) tiếp xúc (d) thì pt có nghiệm kép
-> 4(m+1)^2 = 0 <=> m = -1
c, Cho điểm cố định A có toạ độ A(x0;y0)
Thay vào (d) ta được \(y_0=mx_0-2m-1\Leftrightarrow\left(x_0-2\right)m-\left(1+y_0\right)=0\Leftrightarrow\left\{{}\begin{matrix}x_0=2\\y_0=-1\end{matrix}\right.\)
Vậy (d) luôn đi qua điểm cố định A(2;1)
a) bạn tự vẽ nha
b) Phương trình hoành độ giao điểm :
\(-\dfrac{1}{4}x^2=mx-2m-1\)
<=> \(x^2+4mx-8m-4=0\)
\(\Delta=\left(4m\right)^2-4\left(-8m-4\right).1=16m^2+32m+16\)
d tiếp xúc (p) khi \(\Delta=16m^2+32m+16=16\left(m+1\right)^2=0\Leftrightarrow m=-1\)
c) Gọi điểm A(x1 ; y1)
Khi đó y1 = mx1 - 2m - 1
<=> mx1 - 2m - 1 - y1 = 0
<=> m(x1 - 2) + (-y1 - 1) = 0
<=> \(x_1=2;y_1=-1\)
=> thử vào (p) => -1 = 1/4 . (22) (đúng)
Vậy A(2 ; -1)

Bài 6:
Xét ΔACB có \(\widehat{A}+\widehat{C}+\widehat{B}=180^0\)
=>\(\widehat{C}+51^0+30^0=180^0\)
=>\(\widehat{C}=180^0-81^0=99^0\)
Xét ΔCAB có
\(\dfrac{AB}{sinC}=\dfrac{AC}{sinB}\)
=>\(\dfrac{AB}{sin99}=\dfrac{224}{sin30}\)
=>\(AB\simeq442,48\left(m\right)\)
Bài 7:
a: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại trung điểm của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>OBAC là tứ giác nội tiếp
=>O,B,A,C cùng thuộc một đường tròn
b: Xét (O) có
ΔCDN nội tiếp
CD là đường kính
Do đó: ΔCND vuông tại N
=>CN\(\perp\)ND tại N
=>CN\(\perp\)AD tại N
Xét ΔDCA vuông tại C có CN là đường cao
nên \(AN\cdot AD=AC^2\left(3\right)\)
Xét ΔACO vuông tại C có CH là đường cao
nên \(AH\cdot AO=AC^2\left(4\right)\)
Từ (3) và (4) suy ra \(AN\cdot AD=AH\cdot AO\)

3,
Ta có
\(\tan\widehat{ABH}=\tan41,5^0=\dfrac{AH}{BH}\approx1\Leftrightarrow AH\approx BH\)
\(\tan\widehat{ACH}=\tan32^0=\dfrac{AH}{CH}\approx1\Leftrightarrow AH\approx CH\)
Vậy \(AH\approx\dfrac{BH+CH}{2}=\dfrac{BC}{2}=150\left(m\right)\)
4, Bài này mình làm tròn đến hàng đơn vị nhé
\(\tan\widehat{B}=\tan30^0=\dfrac{AH}{BH}=\dfrac{\sqrt{3}}{3}\Leftrightarrow AH=\dfrac{\sqrt{3}BH}{3}\)
\(\tan\widehat{ACH}=\tan35^0=\dfrac{AH}{CH}\approx1\Leftrightarrow AH\approx CH\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{3}BH\approx CH\)
Mà \(BH-CH=BC=1500\Leftrightarrow BH-\dfrac{\sqrt{3}}{3}BH=1500\)
\(\Leftrightarrow\dfrac{3-\sqrt{3}}{3}BH=1500\\ \Leftrightarrow\left(3-\sqrt{3}\right)BH=4500\\ \Leftrightarrow BH=\dfrac{4500}{3-\sqrt{3}}=\dfrac{4500\left(3+\sqrt{3}\right)}{6}=750\left(3+\sqrt{3}\right)\left(cm\right)\)
\(\Leftrightarrow AH=\dfrac{\sqrt{3}}{3}BH=\dfrac{\sqrt{3}}{3}\cdot750\left(3+\sqrt{3}\right)=250\sqrt{3}\left(3+\sqrt{3}\right)\\ AH=750\sqrt{3}+750\left(cm\right)\)
Vậy ...

 giúp tui bài 1 với :3
giúp tui bài 1 với :3
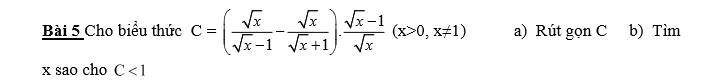
 giúp tui bài 6 với mng ơiiiiiii!
giúp tui bài 6 với mng ơiiiiiii!

