K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
0
5 tháng 1 2016
\(N=\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{10^2}\)
\(N>\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{10.11}\)
\(N>\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-....-\frac{1}{11}=\frac{1}{2}-\frac{1}{11}=\frac{10}{22}>\frac{9}{22}\)
Vậy N > 9/22
31 tháng 8 2020
a) Quy đồng pso và tính như bthg (4824829/6350400)
b) Vì 4814819 < 6350400 => A < 1
NM
2
N
9 tháng 10 2018
A = 1 + 4 + 9 + 16 +....+ 64 + 81 + 100
=>A = 1 + 1 + 3 + 1 + 8 +...+ 1 + 63 + 1 + 80 + 1 + 99
=>A = 1 + 1 + ..... + 1 + 3 + 8 + 14 +....+80 + 99
Bạn tự tìm kết quả nhé
Hok tốt
9 tháng 10 2018
A=(1+9)+(4+16)+(9+81)+(16+64)+(25+36+49+100)
A=10+20+90+80+(61+49+100)
A=10+20+90+80+110+100
A=(100+10)+(20+90)+80+110
A=110+110+110+80
A=(110.3)+80
A=330+80
A=410
t i c k cho mình nha
bạnnnnnnnnnnnnnnnnnnnnn
NP
3
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
1 tháng 12 2023
A = \(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{16}\) + \(\dfrac{1}{32}\)
2 \(\times\) A = 1 + \(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{16}\)
2 \(\times\) A - A = 1 + \(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{16}\) - (\(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{16}\) + \(\dfrac{1}{32}\))
A = 1 + \(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{16}\) - \(\dfrac{1}{2}\) - \(\dfrac{1}{4}\) - \(\dfrac{1}{8}\) - \(\dfrac{1}{16}\) - \(\dfrac{1}{32}\)
A = 1 - \(\dfrac{1}{32}\)
A = \(\dfrac{31}{32}\)
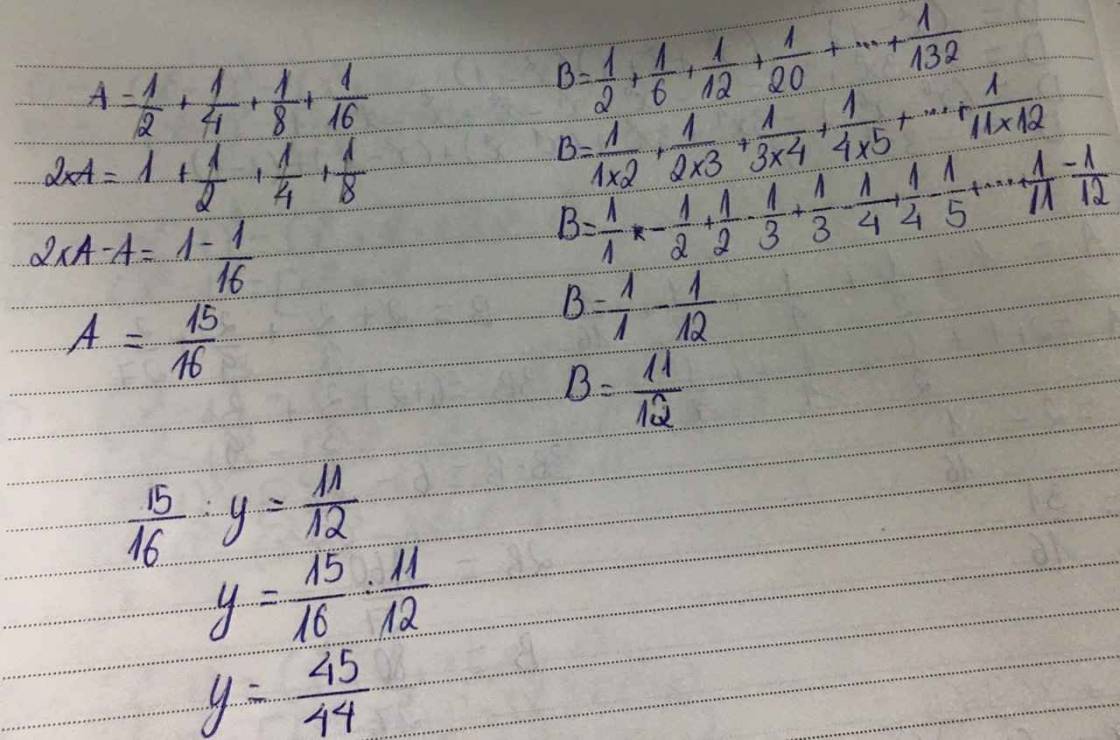
xí nha!đây ko phải toán lớp 5 nha bạn !
cô giáo mình ra đề như vậy mà