Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\left\{{}\begin{matrix}mp\left(ABCD\right):AB//CD\\mp\left(CDD'C'\right):CD//C'D'\end{matrix}\right.\left(\text{Tính chất hình chữ nhật}\right)\)
\(\Rightarrow AB//C'D'\left(\text{Cùng song song với CD}\right)\)
b) \(\left\{{}\begin{matrix}mp\left(ABCD\right):AD//BC\\mp\left(BCC'B'\right):BC//B'C'\end{matrix}\right.\left(\text{Tính chất hình chữ nhật}\right)\)
\(\Rightarrow AD//B'C'\left(\text{Cùng song song với BC}\right)\)
c) \(\left\{{}\begin{matrix}mp\left(ADD'A'\right):AA'//DD'\\mp\left(CDD'C'\right):CC'//DD'\end{matrix}\right.\left(\text{Tính chất hình chữ nhât}\right)\)
\(\Rightarrow AA'//CC'\) (Cùng song song với DD')


a) \(\left\{{}\begin{matrix}mp\left(ABCD\right):AB=CD\left(1\right)\\mp\left(ABB'A'\right):AB=A'B'\left(2\right)\\mp\left(CDD'C'\right):CD=C'D'\left(3\right)\\mp\left(A'B'C'D'\right):A'B'=C'D'\left(4\right)\end{matrix}\right.-\text{Tính chất hình chữ nhật}\)
Từ (1) và (3) => \(AB=CD=C'D'\) (*)
Từ (2) và (4) => \(AB=A'B'=C'D'\) (**)
Vậy từ(*) và (**) suy ra : \(AB=CD=C'D'=A'B'\)
b) \(C'D'//CD\Leftrightarrow\left\{{}\begin{matrix}C'D'\in mp\left(CDD'C'\right)\\CD\in\left(CDD'C'\right)\\\text{Không có điểm chung}\end{matrix}\right.\)
c) * \(AD//mp\left(BCC'B'\right)\) vì :
\(\left\{{}\begin{matrix}AD\notin mp\left(BCC'B'\right)\\AD//BC\end{matrix}\right.\)
* \(AD//mp\left(A'B'C'D'\right)\) vì :
\(\left\{{}\begin{matrix}AD\notin mp\left(A'B'C'D'\right)\\AD//A'D'\end{matrix}\right.\)
d) \(mp\left(ADD'A'\right)//mp\left(BCC'B'\right)\)

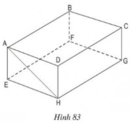
a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).



1:
a: AB=CD=A'B'=C'D'
b: C'D'//CD vì CDD'C là hình bình hành
c: AD//(B'BCC')
AD//(A'B'C'D')