Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tương tự 1A
a) AB' và C'D song song, B'D' và AD chéo nhau, AC và A'C' song song.
b) BC' song song với (ADD'A').
c) AC' và CA' cắt nhau tại C.
d) (ACC'A') và (BDD'B') cắt nhau theo giao tuyến OO' (O và O' lần lượt là giao của AC, BD và A'C', B'D')
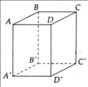

a) BB' và A'D' chéo nhau, CD và B'C' chéo nhau.
b) AB song song với CD (hoặc A'B')
c) (ABB'A') cắt (BDD'B') theo giao tuyến BB', (ABB'A')// (CDD'C') vì AB và AA' song song với (CDD'C').
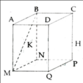

* Cách vẽ:
- Kẻ tỉa Ax bất kì khác tia AB, AC
- Trên tia Ax, lấy hai điểm E và F sao cho AE = 2 (đơn vị dài), EF = 3 (đơn vị dài)
- Kẻ đường thẳng FB
- Từ E kẻ đường thẳng song song với FB Cắt AB tại M.
- Kẻ đường thẳng FC.
- Từ E kẻ đường thẳng song song với FC cắt AC tại N.
Ta có M, N là hai điểm cần vẽ.
* Chứng minh:
Trong △ ABC, ta có:
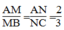
Suy ra: MN // BC (Theo định lí đảo của định lí Ta-lét)

A) xét tứ giác OCKB :có BK song song với OC( vì BK song song với AC)
: có CK song song với OB ( vì CK song song vớiOB)
Từ hai điều kiện trên ta kết luận tứ giác OCKB là hình bình hành
mà ta lạ có góc COB=90 độ
vậy tứ giác OCKC là hình chữ nhật
B) Ta có : BK song song với OA ( vì BK song song song với AC)
Hơn nữa BK lại bằng OC ( vì OCBK là hình chữ nhật)
Mà OC lại bằng OA suy ra BK=OA
từ những điều kiện trên suy ra tứ giác ABKO là HBH
vậy AB=OK
C)nếu cần tìm điều kiện ở tứ giác ABCD để thỏa mãn tứ giác OBKC là hình vuông thì ta sẽ chọn điều kiện đó là
tứ giác ABCD là hình vuông

a: Xét tứ giác OBKC có
OB//KC
OC//BK
góc BOC=90 độ
Do đó: OBKC là hình chữ nhật
b: OBKC là hình chữ nhật
nên OK=BC
=>OK=AB
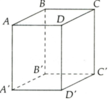



D A B C A' B' C' D'
a) \(\left\{{}\begin{matrix}mp\left(ABCD\right):AB//CD\\mp\left(CDD'C'\right):CD//C'D'\end{matrix}\right.\left(\text{Tính chất hình chữ nhật}\right)\)
\(\Rightarrow AB//C'D'\left(\text{Cùng song song với CD}\right)\)
b) \(\left\{{}\begin{matrix}mp\left(ABCD\right):AD//BC\\mp\left(BCC'B'\right):BC//B'C'\end{matrix}\right.\left(\text{Tính chất hình chữ nhật}\right)\)
\(\Rightarrow AD//B'C'\left(\text{Cùng song song với BC}\right)\)
c) \(\left\{{}\begin{matrix}mp\left(ADD'A'\right):AA'//DD'\\mp\left(CDD'C'\right):CC'//DD'\end{matrix}\right.\left(\text{Tính chất hình chữ nhât}\right)\)
\(\Rightarrow AA'//CC'\) (Cùng song song với DD')