Tìm m để hàm số y = - 2x^2- (2m - 1)x + 6 - 3m nghịch biến trong khoảng (-2 ; dương vô cùng)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 3 2023
a.
Hàm số nghịch biến khi \(x< 0\Rightarrow-3m-2>0\Rightarrow m< -\dfrac{2}{3}\)
b.
Do \(a=m^2-2m+3=\left(m-1\right)^2+2>0;\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
c.
Hàm đồng biến khi \(x>0\Rightarrow2m+3>0\)
\(\Rightarrow m>-\dfrac{3}{2}\)
CM
26 tháng 9 2018
Đáp án D
Có y ' = m m + 1 − 2 m + 2 x + m 2 = m 2 − m − 2 x + m 2 .
Hàm số xác định trên
− 1 ; + ∞ ⇔ − m ∉ − 1 ; + ∞ ⇔ − m ≤ − 1 ⇔ m ≥ 1
Khi đó hàm số ngịch biến trên
− 1 ; + ∞ ⇔ y ' < 0 ∀ x ∈ − 1 + ∞ ⇔ m 2 − m − 2 < 0 ⇔ m ∈ − 1 ; 2
Vậy m ∈ 1 ; 2 .
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 7 2021
3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)
12 tháng 11 2023
a: TXĐ: D=R\{-1}
\(y'=\dfrac{\left(x+m\right)'\left(x+1\right)-\left(x+1\right)'\left(x+m\right)}{\left(x+1\right)^2}\)
\(=\dfrac{x+1-x-m}{\left(x+1\right)^2}=\dfrac{1-m}{\left(x+1\right)^2}\)
Để hàm số nghịch biến trên từng khoảng xác định thì \(y'< 0\forall x\)
=>\(\dfrac{1-m}{\left(x+1\right)^2}< 0\)
=>1-m<0
=>m>1
b: TXĐ: D=R\{m}
\(y=\dfrac{2x-3m}{x-m}\)
=>\(y'=\dfrac{\left(2x-3m\right)'\left(x-m\right)-\left(2x-3m\right)\left(x-m\right)'}{\left(x-m\right)^2}\)
\(=\dfrac{2\left(x-m\right)-\left(2x-3m\right)}{\left(x-m\right)^2}=\dfrac{2x-2m-2x+3m}{\left(x-m\right)^2}\)
\(=\dfrac{m}{\left(x-m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì \(y'>0\forall x\)
=>\(\dfrac{m}{\left(x-m\right)^2}>0\)
=>m>0
27 tháng 5 2021
a) Để hàm đồng biến <=> a>0 <=> m-1>0 <=> m>1
Để hàm nghịch biến <=> a<0 <=> m<1
b)Có phải đề như này: \(y=-m^2x+1\)
Nhận xét: \(-m^2\le0\forall m\)
=> Hàm luôn nghịch biến với mọi \(m\ne0\)
c)Để hàm nghịch biến <=> a<0 <=> 1-3m<0\(\Leftrightarrow m>\dfrac{1}{3}\)
Để hàm đồng biền <=> a>0 \(\Leftrightarrow m< \dfrac{1}{3}\)
TK
27 tháng 5 2021
a/ Hàm số y=(m-1)x+2 đồng biến khi và chỉ khi m-1>0
⇔m>1
nghịch biến khi và chỉ khi m-1<0
⇔m<1
b/Hàm số y=-2mx+1 đồng biến khi và chỉ khi -2m>0
⇔m<0
nghịch biến khi và chỉ khi -2m<0
⇔m>0
c/Hàm số y=(1-3m)x+2m đồng biến khi và chỉ khi 1-3m>0
⇔-3m>-1
⇔m<\(\dfrac{1}{3}\)
nghịch biến khi và chỉ khi 1-3m<0
⇔-3m<-1
⇔m>\(\dfrac{1}{3}\)
.
.
.
.
CM
31 tháng 5 2019
Chọn B
Tập xác định của hàm số: 
Ta có: 
.
.
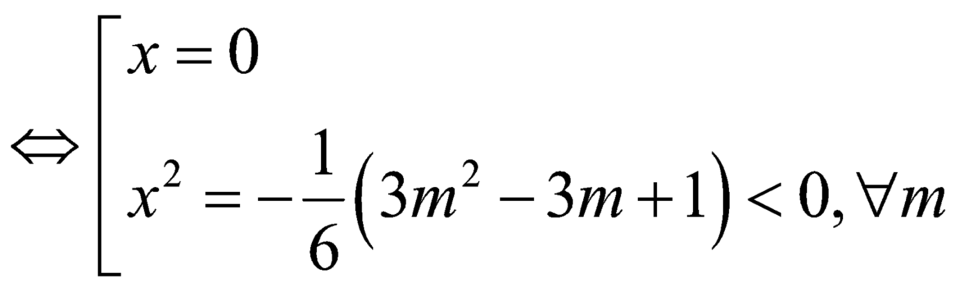
Vì 
nên hàm số nghịch biến trên khoảng 
.
CM
25 tháng 4 2019
Đáp án D
y = m x − 2 − 2 x + m ⇒ y ' = m 2 − 4 ( − 2 x + m ) 2 y ' < 0 ⇒ − 2 < m < 2
Suy ra, hàm số nghịch biến trên ( − ∞ ; m 2 ) và ( m 2 ; + ∞ )
⇒ m 2 ≤ 1 2 ⇒ m ≤ 1 ⇒ − 2 < m ≤ 1
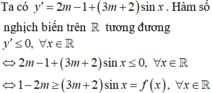
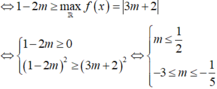
Xét parabol \(\left(C_m\right):y=-2x^2-\left(2m-1\right)x+6-3m\), ta có \(\Delta=\left[-\left(2m-1\right)\right]^2-4\left(-2\right)\left(6+3m\right)=4m^2+20m+49\)
Gọi \(I_m\) là đỉnh của \(\left(C_m\right)\) thì \(I_m\left(\dfrac{-2m+1}{4};\dfrac{4m^2+20m+49}{8}\right)\)
Để hàm số đã cho nghịch biến trong khoảng \(\left(-2;+\infty\right)\) thì \(\dfrac{-2m+1}{4}=-2\Leftrightarrow m=\dfrac{9}{2}\)
Tao đéo biết thằng Nguyễn Huy Hung nha ☹