Cho Parabol (P): y= x2- 2( m- 1) x + m2 - m. Tìm giá trị của m để (P) cắt ox tại 2 điểm phân biệt
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét phương trình hoành độ giao điểm: x2 – 2x + m – 1 = 0
Để parabol cắt Ox tại hai điểm phân biệt có hoành độ dương thì phương trình có hai nghiệm dương hay 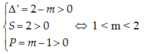
Chọn A.

a: Thay x=0 và y=-5 vào (d), ta được:
2(m+1)*0-m^2-4=-5
=>m^2+4=5
=>m=1 hoặc m=-1
b:
PTHĐGĐ là;
x^2-2(m+1)x+m^2+4=0
Δ=(2m+2)^2-4(m^2+4)
=4m^2+8m+4-4m^2-16=8m-12
Để PT có hai nghiệm phân biệt thì 8m-12>0
=>m>3/2
x1+x2=2m+2; x1x2=m^2+4
(2x1-1)(x2^2-2m*x2+m^2+3)=21
=>(2x1-1)[x2^2-x2(2m+2-2)+m^2+4-1]=21
=>(2x1-1)[x2^2+2x2-x2(x1+x2)+x1x2-1]=21
=>(2x1-1)(x2^2+2x2-x1x2-x2^2+x1x2-1]=21
=>(2x1-1)(2x2-1)=21
=>4x1x2-2(x1+x2)+1=21
=>4(m^2+4)-2(2m+2)+1=21
=>4m^2+16-4m-4-20=0
=>4m^2-4m-8=0
=>(m-2)(m+1)=0
=>m=2(nhận) hoặc m=-1(loại)

PTHĐGĐ là;
x^2-6x+m-3=0
Δ=(-6)^2-4(m-3)=36-4m+12=-4m+48
Để PT có hai nghiệm phân biệt thì -4m+48>0
=>m<12
(x1-1)(x2^2-x2(x1+x2-1)+x1x2-1)=2
=>(x1-1)(-x1x2+x2+x1x2-1)=2
=>x1x2-(x1+x2)+1=2
=>m-3-6+1=2
=>m-8=2
=>m=10

a: PTHĐGĐ là:
x^2+mx-m-2=0(1)
Khi m=2 thì (1) sẽ là
x^2+2x-2-2=0
=>x^2+2x-4=0
=>\(\left[{}\begin{matrix}x=-1+\sqrt{5}\\x=-1-\sqrt{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=6-2\sqrt{5}\\y=6+2\sqrt{5}\end{matrix}\right.\)
b: Δ=m^2-4(-m-2)
=m^2+4m+8
=(m+2)^2+4>0 với mọi x
=>(d) luôn cắt (P) tại hai điểm phân biệtx
x1^2+x2^2=7
=>(x1+x2)^2-2x1x2=7
=>(-m)^2-2(-m-2)=7
=>m^2+2m+4-7=0
=>m^2+2m-3=0
=>m=-3 hoặc m=1

- xét phương trình hoành độ giao điểm : \(x^2=\left(2m-1\right)x-m+2\)\(\Leftrightarrow x^2-\left(2m-1\right)x+m-2=0\)có \(\Delta=\left(2m-1\right)^2-4\left(m-2\right)=4m^2-8m+9=\left(2m-1\right)^2+8\ge8\)vậy nên phương trinh luôn có 2 nghiệm phân biệt tức hai đồ thị luôn cắt nhau tại 2 điểm phân biệt A và B
- Có viet : \(\hept{\begin{cases}x_1+x_2=2m-1\\x_1x_2=m-2\end{cases}}\)ta có : \(A\left(x_1,y_1\right)=A\left(x_1,x_1^2\right)\)và \(B\left(x_2,y_2\right)=B\left(x_2,x_2^2\right)\)
nên ta có : \(x_1y_1+x_2y_2=0\Leftrightarrow x_1^3+x_2^3=0\)\(\Leftrightarrow\left(x_1+x_2\right)\left(\left(x_1+x_2\right)^2-3x_1x_2\right)=0\)\(\Leftrightarrow\left(2m-1\right)\left[\left(2m-1\right)^2-3m+6\right]=0\)
- \(2m-1=0\Leftrightarrow m=\frac{1}{2}\)
- \(\left(2m-1\right)^2-3m+6=0\Leftrightarrow4m^2-7m-7=0\)VN
2. Cho parabol (P): y = x2 và đường thẳng (d): y = 2(m – 1)x + m2 + 2m (m là tham số, m ∈ R )
a) Chứng minh rằng đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt A, B?
b) Gọi H và K lần lượt là hình chiếu của A và B trên trục hoành.
Tìm m sao cho: OH2 + OK2 = 6 mọi người hướng dẫ mk ý b vs

Phương trình hoành độ giao điểm d và (P):
\(-2x^2=x-m\Leftrightarrow2x^2+x-m=0\) (1)
(d) cắt (P) tại 2 điểm pb khi (1) có 2 nghiệm pb
\(\Leftrightarrow\Delta=1+8m>0\Leftrightarrow m< -\dfrac{1}{8}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{1}{2}\\x_1x_2=-\dfrac{m}{2}\end{matrix}\right.\)
\(x_1+x_2=x_1x_2\Leftrightarrow-\dfrac{1}{2}=-\dfrac{m}{2}\Leftrightarrow m=1\)

Phương trình hoành độ giao điểm là:
\(x^2-mx+2m-4=0\)
\(\Delta=\left(-m\right)^2-4\left(2m-4\right)\)
\(=m^2-8m+16=\left(m-4\right)^2\)
Để (P) cắt (d) tại hai điểm phân biệt thì m-4<>0
hay m<>4
Ta có: \(x_1^2+x_2^2\)
\(=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=m^2-2\left(2m-4\right)\)
\(=m^2-4m+8\)
\(=\left(m-2\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi m=2

Phương trình hoành độ giao điểm là:
\(x^2-2\left(m-1\right)x+m^2-m=0\)
\(\Delta=\left(2m-2\right)^2-4\left(m^2-m\right)\)
\(=4m^2-8m+4-4m^2+4m=-4m+4\)
Để (P) cắt Ox tại 2 điểm phân biệt thì \(\Delta>0\)
=>-4m+4>0
=>-4m>-4
=>m<1