Cho hình thoi ABCD: AC=5,4cm; BD=6,8cm. Trên các cạnh AB, CD lần lượt lấy điểm M, N sao cho AMND là hình bình hành. Xác định vị trí điểm N để diện tích hình bình hành AMND=6,12 cm vuông.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
Vì tứ giác ABCD là hình thoi có 2 đường chéo AC= BD nên tứ giác ABCD là hình vuông ( dấu hiệu nhận biết hình vuông)..
Gọi O là tâm hình vuông.
Theo tính chất hình vuông ta có:
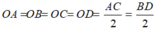
Do đó, O là tâm đường tròn ngoại tiếp hình vuông ABCD.

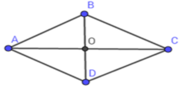
Gọi \(O\) là giao điểm của \(AC\)và \(BD\).
Theo đề ta có: \(\hept{\begin{cases}AC=8cm\\BD=6cm\end{cases}}\)
Theo tính chất của hình thoi ta có: \(\hept{\begin{cases}AO=OC=4cm\\BO=OD=3cm\end{cases}}\)
Áp dụng định lí Pitago trong \(\Delta AOB\) có:
\(AB^2=AO^2+OB^2\)
\(\Rightarrow AB=\sqrt{AO^2+OB^2}=\sqrt{4^2+6^2}\)
\(\Rightarrow AB=5cm\)
\(\Rightarrow S_{ABCD}=4AB=4.5=20cm\)
Vậy ...............

đáy lớn DC của hình thang ABCD là:
5.4 * 3 =16.2 (cm)
đường cao AH của hình thang ABCD là:
5.4 : 4 * 3 =4.05 (cm)
diện tích hình thang ABCDlà:
(16.2 + 5.4) * 4.05 : 2 =43.74(cm2)
đáp số 43.72cm2

Ta có: AC = 2AO = 2.12 = 24cm
SABCD = 1 2 BD.AC
=> BD = 2 S A B C D A C = 2.168 24 =14(cm)
=> BO = 1 2 BD = 1 2 .14 = 7(cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
AB = A O 2 + B O 2 = 12 2 + 7 2 = 193 (cm)
Đáp án cần chọn là: C
Diện tích hình thoi ABCD là: 5,4 x 6,8 : 2 = 18,36 (cm2)
Diện tích hình thoi ABCD gấp diện tích hình bình hành AMND số lần là: 18,36 : 6,12 = 3 (lần)
⇒ PN = \(\dfrac{1}{3}\) PC