2x + 2x = 48
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BJ
1
9 tháng 8 2016
\(x=3y=2z\)
\(\Rightarrow\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\)
\(\Rightarrow\frac{2x}{2}=\frac{3y}{6}=\frac{4z}{12}=\frac{2x-3y+4z}{2-6+12}=\frac{48}{8}=6\)
Rồi thế vào là ra thôi :
\(\frac{2x}{2}=6\Rightarrow x=..........\)
Rồi tương tự thôi
TN
4
IM
9 tháng 8 2016
6)
\(x=3y=2z\)
\(\Rightarrow\frac{x}{6}=\frac{y}{2}=\frac{z}{3}\)
\(\Rightarrow\frac{2x}{12}=\frac{3y}{6}=\frac{4z}{12}\)
Áp dụng tc của dãy tỉ số bằng nhau ta có
\(\frac{2x}{12}=\frac{3y}{6}=\frac{4z}{12}=\frac{2x-3y+4z}{12-6+12}=\frac{48}{18}=\frac{24}{9}\)
\(\Rightarrow\begin{cases}x=16\\y=\frac{16}{3}\\z=8\end{cases}\)
IM
9 tháng 8 2016
7)
\(2x=3y=-2z\)
\(\Rightarrow\frac{2x}{1}=\frac{3y}{1}=\frac{-4z}{2}\)
Áp dụng tc của dãy tỉ số bằng nhau ta có
\(\frac{2x}{1}=\frac{3y}{1}=\frac{-4z}{2}=\frac{2x-3y-\left(-4z\right)}{1-1-2}=\frac{48}{-2}=-24\)
\(\Rightarrow\begin{cases}x=-12\\y=-8\\z=12\end{cases}\)
T
29 tháng 9 2023
\(\left(2x-4\right)^{38}=\left(2x-4\right)^{48}\)
\(\Rightarrow\left(2x-4\right)^{38}-\left(2x-4\right)^{48}=0\)
\(\Rightarrow\left(2x-4\right)^{38}\left[1-\left(2x-4\right)^{10}\right]=0\)
\(\Rightarrow\left[{}\begin{matrix}\left(2x-4\right)^{38}=0\\1-\left(2x-4\right)^{10}=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x-4=0\\\left(2x-4\right)^{10}=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=4\\2x-4=1\\2x-4=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\2x=5\\2x=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{5}{2}\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy \(x\in\left\{2;\dfrac{5}{2};\dfrac{3}{2}\right\}.\)
#\(Toru\)
KM
0
S
6 tháng 9 2017
\(\frac{2x}{1}=\frac{3y}{1}=\frac{-4z}{2}=\frac{2x-3y+4z}{1-1-2}=\frac{48}{-2}=-24\)
=> \(\hept{\begin{cases}2x=-24\\3y=-24\\-2z=-24\end{cases}\Rightarrow\hept{\begin{cases}x=-12\\y=-8\\z=12\end{cases}}}\)
6 tháng 9 2017
\(2c=3y=-2zz\)
\(\Rightarrow\frac{2x}{1}=\frac{3y}{2}=\frac{-4z}{2}\)
Áp dụng tính chất của tỉ số bằng nhau ta có :
\(\frac{2x}{1}=\frac{3y}{1}=\frac{-4z}{2}=\frac{2x-3y-\left(-4z\right)}{1-1-2}=\frac{48}{-2}=-24\)
\(\Rightarrow\hept{\begin{cases}x=-12\\y=-8\\z=12\end{cases}}\)
17 tháng 7 2023
a) \(2^x=8.64=2^3.2^6=2^9\Rightarrow x=9\)
b) \(3.2^x=48\Rightarrow2^x=16=2^4\Rightarrow x=4\)
VN
Võ Ngọc Phương
VIP
22 tháng 9 2023
\(2^{2x}+2^{2x+1}=48\)
\(2^{2x}+2^{2x}.2=48\)
\(2^{2x}.\left(1+2\right)=48\)
\(2^{2x}.3=48\)
\(2^{2x}=48:3\)
\(2^{2x}=16\)
\(2^{2x}=2^4\)
\(\Rightarrow2x=4\)
\(x=4:2\)
\(x=2\)
24 tháng 2 2023
Ta có:
\(2x=3y=-2z\) hay \(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{z}{-3}\)
Từ \(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{z}{-3}\) suy ra \(\dfrac{2x}{6}=\dfrac{3y}{6}=\dfrac{4z}{-12}\)
Áp dụng tính chất cơ bản của phân số, ta có:
\(\dfrac{2x}{6}=\dfrac{3y}{6}=\dfrac{4z}{-12}=\dfrac{2x-3y+4z}{6-6+\left(-12\right)}=\dfrac{48}{-12}=-4\)
\(\Rightarrow x=-4\cdot3=-12\)
\(\Rightarrow y=-4\cdot2=-8\)
\(\Rightarrow z=\left(-4\right)\cdot\left(-3\right)=12\)
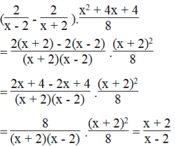
`2^x +2^x =48`
`2^x (1+1)=48`
`2^x *2 =48`
`2^x = 48/2 =24`
`=> x in emptyset`
2x + 2x = 48
2x. ( 1 + 1 ) = 48
2x.2 = 48
2x = 48 : 2
2x = 24
x = log224