Tập nghiệm nguyên của bất phương trình; \(\sqrt{x+2}>x\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 4 2020
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
7 tháng 4 2020
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
V
0
CM
5 tháng 8 2018
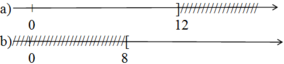
a) Hình a) biểu diễn tập nghiệm của bất phương trình:
x ≤ 12 hoặc x + 4 ≤ 16 hoặc 2x + 1 ≤ 25
b) Hình biểu diễn tập nghiệm của bất phương trình:
x ≥ 8 hoặc x + 3 ≥ 11 hoặc 3 – 2x ≤ -13.
CM
11 tháng 3 2017
Có 
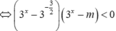
+) Nếu
m
≤
0
bất phương trình tương đương với 
chứa vô số các số nguyên (loại);
+) Nếu 0 < m < 3 - 3 2 không có số nguyên m nào cả (loại).
+) Nếu
m
>
3
-
3
2
bất phương trình tương đương với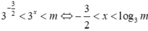 
Tập nghiệm là 
Vì S chứa đúng 10 số nguyên do đó 
⇒
m
∈
3
8
+
1
,
.
.
.
,
3
9
Có tất cả
3
9
-
3
8
số nguyên thoả mãn.
Chọn đáp án D.
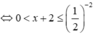
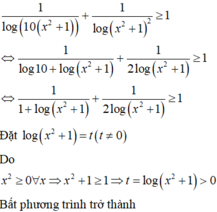
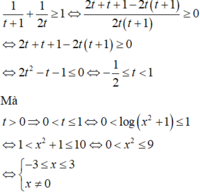
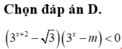
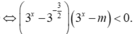
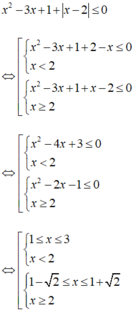
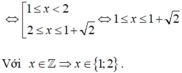
<=> \(\left(\sqrt{x+2}\right)^2\)> x2
<=> \(x+2>x^2\)
<=> \(-\left(x^2-x-2\right)>0\)
<=>\(x^2-x-2< 0\)
<=> \(x^2-2x+x-2< 0\)
<=> \(\left(x-2\right)\left(x+1\right)< 0\) vì 2 tích nhân với nhau nhỏ hơn 0 nên
<=> \(\orbr{\begin{cases}x-2>0\\x+1< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>2\\x< -1\end{cases}}\)
và \(\orbr{\begin{cases}x-2< 0\\x+1>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 2\\x>-1\end{cases}}\)
Mình nhập 0;1 nó cho sai!!