
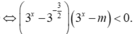

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

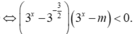


Chọn đáp án D.
Bất phương trình tương đương với
![]()
![]()
![]()
![]()
![]()
trong đó hàm số f t = t 3 + 3 t đồng biến trên R
Vậy y c b t ⇔ x 2 - m x + 1 ≥ 0 , ∀ x
![]()
Có 5 số nguyên thoả mãn

Chọn C.
Bất phương trình
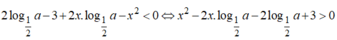
Đặt , 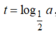 khi đó bất phương trình trở thành x2-2tx-2t+3> 0 (*)
khi đó bất phương trình trở thành x2-2tx-2t+3> 0 (*)
Bất phương trình (*) nghiệm đúng với mọi x khi và chỉ khi
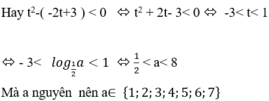
Vậy có tất cả 7 giá trị nguyên của a thỏa mãn yêu cầu bài toán.

\(\Leftrightarrow\left\{{}\begin{matrix}3.2^xlogx-12logx-2^x+4=0\left(1\right)\\5^x=m\left(2\right)\end{matrix}\right.\) và \(5^x\ge m\) (\(x>0\))
Xét (1):
\(\Leftrightarrow3logx\left(2^x-4\right)-\left(2^x-4\right)=0\)
\(\Leftrightarrow\left(3logx-1\right)\left(2^x-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x_1=2\\x_2=\sqrt[3]{10}\end{matrix}\right.\)
\(y=5^x\) đồng biến trên R nên (2) có tối đa 1 nghiệm
Để pt đã cho có đúng 2 nghiệm phân biệt ta có các TH sau:
TH1: (2) vô nghiệm \(\Rightarrow m\le0\) (ko có số nguyên dương nào)
TH2: (2) có nghiệm (khác với 2 nghiệm của (1)), đồng thời giá trị của m khiến cho đúng 1 nghiệm của (1) nằm ngoài miền xác định
(2) có nghiệm \(\Rightarrow m>0\Rightarrow x_3=log_5m\)
Do \(\sqrt[3]{10}>2\) nên bài toán thỏa mãn khi: \(x_1< x_3< x_2\)
\(\Rightarrow2< log_5m< \sqrt[3]{10}\)
\(\Rightarrow25< m< 5^{\sqrt[3]{10}}\) (hơn 32 chút xíu)
\(\Rightarrow\) \(32-26+1\) giá trị nguyên

Chọn C
![]()
![]()
![]()
![]()
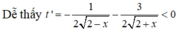
nên hàm t = t (x) nghịch biến trên (-2;2)
![]()
![]()
Thay vào bất phương trình trên được:
![]()
![]()
Bất phương trình đã cho nghiệm đúng với mọi x ∈ - 2 ; 2 nếu và chỉ nếu bất phương trình
![]()
nghiệm đúng với mọi t ∈ - 6 ; 2
tam thức bậc hai f t = 2 t 2 - m t + 3 m - 5 có hai nghiệm thỏa mãn
![]()
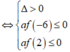
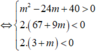
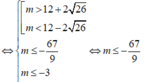
Kết hợp với m ∈ - 10 ; 10 thì m ∈ - 10 ; - 9 ; - 8

Chọn A.
Bất phương trình tương đương: 2x > m2 - 10m + 9
Bất phương trình đã cho nghiệm đúng với mọi x khi và chỉ khi :
m2 - 10m + 9 ≤ 0 hay 1 ≤ m ≤ 9
Mà ![]()

Đáp án D.
Ta có:
P T ⇔ m 9 4 x - 2 m + 1 6 4 x + m ≤ 0
⇔ m 3 2 2 x - 2 m + 1 3 2 x + m ≤ 0
Đ ặ t t = 3 2 x ; d o x ∈ 0 ; 1 ⇒ t ∈ 1 ; 3 2 .
Khi đó PT trở thành:
m t 2 - 2 m + 1 t + m ≤ 0 ⇔ m t 2 - 2 t + 1 ≤ t
Rõ ràng t =1 là nghiệm của BPT đã cho.
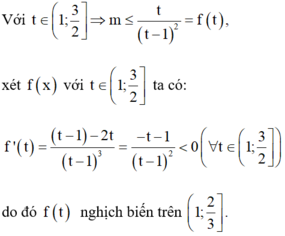
D o đ ó B P T n g h i ệ m đ ú n g v ớ i ∀ t ∈ 1 ; 3 2
⇔ m ≤ M i n 1 ; 3 2 f t = f 3 2 = 6 .
Vậy có 6 giá trị nguyên dương của m thỏa mãn.