Công Thức Lượng Giác
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 1 2017
a) Các hằng đẳng thức lượng giác cơ bản:
sin2α + cos2α = 1
1 + tan2α = 1/(cos2α); α ≠ π/2 + kπ, k ∈ Z
1 + cot2α = 1/(sin2α); α ≠ kπ, k ∈ Z
tanα.cotα = 1; α ≠ kπ/2, k ∈ Z
b) Công thức cộng:
cos(a - b) = cosa cosb + sina sinb
cos(a + b) = cosa cosb - sina sinb
sin(a - b) = sina cosb - cosa sinb
sin(a + b) = sina.cosb + cosa.sinb
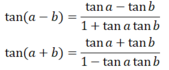
c) Công thức nhân đôi:
sin2α = 2 sinα cosα
cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α
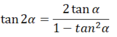
d) Công thức biến đổi tích thành tổng:
cos a cosb = 1/2 [cos(a - b) + cos(a + b) ]
sina sinb = 1/2 [cos(a - b) - cos(a + b) ]
sina cosb = 1/2 [sin(a - b) + sin(a + b) ]
Công thức biến đổi tổng thành tích:
N
1
MK
13 tháng 8 2017
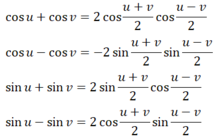
1.Công thức cộng:
sin(x+y)=sinx.cosy+cosx.siny
sin(x-y)=sinx.cosy-cosx.siny
cos(x+y)=cosxcosy-sinxsiny
cos(x-y)=cosxcosy+sinxsiny
tan(x+y)=\(\dfrac{tanx+tany}{1-tanx.tany}\)
tan(x-y)=\(\dfrac{tanx-tany}{1+tanx.tany}\)
2.Công thức nhân đôi:
sin2x=2sinx.cosx
cos2x=cos2x-sin2x=1-2sin2x=2cos2x-1
tan2x=\(\dfrac{2tanx}{1-tan^2x}\)
3. Công thức hạ bậc:
sin2x=\(\dfrac{1-cos2x}{2}\)
cos2x=\(\dfrac{1+cos2x}{2}\)
tan2x=\(\dfrac{1-cos^2x}{1+cos^2x}\)
4. Công thức biến đổi tích thành tổng:
cosx.cosy=\(\dfrac{1}{2}\)[cos(x-y)+cos(x+y)]
sinx.siny=\(\dfrac{1}{2}\)[cos(x-y)-cos(x+y)]
sinx.cosy=\(\dfrac{1}{2}\)[sin(x-y)+sin(x+y)]
5. Công thức biến đổi tổng thành tích:
cosx+cosy=2cos\(\dfrac{x+y}{2}\).cos\(\dfrac{x-y}{2}\)
cosx-cosy=2sin\(\dfrac{x+y}{2}\).sin\(\dfrac{x-y}{2}\)
sinx+siny=2sin\(\dfrac{x+y}{2}\).cos\(\dfrac{x-y}{2}\)
sinx-siny=2cos \(\dfrac{x+y}{2}\).sin \(\dfrac{x-y}{2}\)
PT
1
HQ
Hà Quang Minh
Giáo viên
24 tháng 8 2023
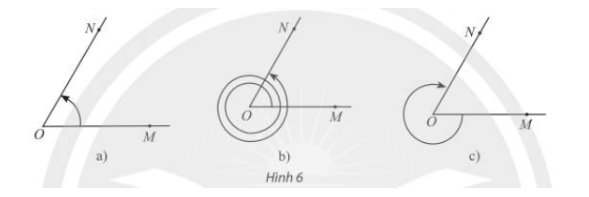
a, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(60^o\)
b, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(60^o+2\cdot360^o=780^o\)
c, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(\dfrac{5}{6}\cdot\left(-360^o\right)=-300^o\)
Công thức tổng quát của số đo góc lượng giác (OM, ON) \(=60^o+360^o\cdot k,k\in Z\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Ta có:
\((O'u',O'v') = (Ou,Ov) + k2\pi \,\, = \, - \frac{{4\pi }}{3}\, + k2\pi \,\,\,\,\,\,\,\,(k \in \mathbb{Z})\)
QT
Quoc Tran Anh Le
Giáo viên
21 tháng 9 2023
\(\begin{array}{l}\cos \left( {\alpha + \alpha } \right) = \cos 2\alpha = \cos \alpha \cos \alpha - \sin \alpha sin\alpha = {\cos ^2}\alpha - {\sin ^2}\alpha \\ = {\cos ^2}\alpha + {\sin ^2}\alpha - 2{\sin ^2}\alpha = 1 - 2{\sin ^2}\alpha = 2{\cos ^2}a - 1\end{array}\)
\(\tan 2\alpha = \tan \left( {\alpha + \alpha } \right) = \frac{{\tan \alpha + \tan \alpha }}{{1 - \tan \alpha .\tan \alpha }} = \frac{{2\tan a}}{{1 - {{\tan }^2}a}}\)
QT
Quoc Tran Anh Le
Giáo viên
21 tháng 9 2023
Ta có:
\(\begin{array}{l}\cos \alpha \cos \beta = \cos \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right) + \cos \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \alpha + \cos \beta } \right)\end{array}\)
\(\begin{array}{l}\sin \alpha \sin \beta = \sin \frac{{\alpha + \beta }}{2}\sin \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right) - \cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \beta - \cos \alpha } \right)\end{array}\)
\(\begin{array}{l}\sin \alpha \cos \beta = \sin \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\sin \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right) + \sin \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\sin \alpha + \sin \beta } \right)\end{array}\)
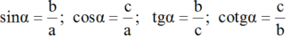
I. Các công thức lượng giác toán 10 cơ bản
Trong phần I, chúng tôi sẽ giới thiệu các công thức lượng giác toán 10 cơ bản nằm trong chương trình sách giáo khoa lớp 10. Đây là những công thức bắt buộc các em học sinh lớp 10 cần phải học thuộc lòng thì mới có thể làm được những bài tập lượng giác cơ bản nhất.
1. Bảng giá trị lượng giác của một số cung hay góc đặc biệt :
2. Hệ thức cơ bản :
3. Cung liên kết :
(cách nhớ: cos đối, sin bù, tan hơn kém pi, phụ chéo)
Đây là những công thức lượng giác toán 10 dành cho những góc có mối liên hệ đặc biệt với nhau như : đối nhau, phụ nhau, bù nhau, hơn kém pi, hơn kém pi/2
• Hai góc đối nhau
cos(–x) = cosx
sin(–x) = – sinx
tan(–x) = – tanx
cot(–x) = – cotx
• Hai góc bù nhau
sin (π - x) = sinx
cos (π - x) = -cosx
tan (π - x) = -tanx
cot (π - x) = -cotx
• Hai góc hơn kém π
sin (π + x) = -sinx
cos (π + x) = -cosx
tan (π + x) = tanx
cot (π + x) = cotx
• Hai góc phụ nhau
4. Công thức cộng :
(cách nhớ : sin thì sin cos cos sin, cos thì cos cos sin sin dấu trừ, tan thì tan nọ tan kia chia cho mẫu số một trừ tan tan) :
6. Công thức nhân ba:
sin3x = 3sinx - 4sin3x
cos3x = 4cos3x - 3cosx
7. Công thức hạ bậc:
8. Công thức tính tổng và hiệu của sin a và cos a:
11. Công thức biến đổi tích thành tổng :