Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

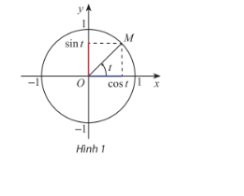
a) Ta thấy \(\sin t = {y_M}\) là tung độ của điểm M trên đường tròn lượng giác và c\(\cos t = {x_M}\) là hoành độ của điểm M trên đường tròn lượng giác.
Với mỗi điểm M xác định, ta chỉ có 1 tung độ và hoành độ duy nhất
Nên ta chỉ xác định duy nhất giá trị sint và cost.
b,
Nếu \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\), ta có: \(\tan t = \frac{{\sin t}}{{{\rm{cost}}}} = \frac{{{y_M}}}{{{x_M}}}\)( \({x_M} \ne 0\))
Nếu \(t \ne k\pi ,k \in \mathbb{Z}\), ta có: \(\cot t = \frac{{{\rm{cost}}}}{{{\rm{sint}}}} = \frac{{{x_M}}}{{{y_M}}}\)( \({y_M} \ne 0\))
Do \({x_M}\), \({y_M}\)xác định duy nhất nên \(\tan t\), \(\cot t\)xác định duy nhất.

Ta có:
\(\cos {15^0} = \cos \left( {{{45}^0} - {{30}^0}} \right) = \cos {45^0}\cos {30^0} + \sin {45^0}\sin {30^0} = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 3 }}{2} + \frac{{\sqrt 2 }}{2}.\frac{1}{2} = \frac{{\sqrt 6 + \sqrt 2 }}{4}\)
\(\sin {15^0} = \sin \left( {{{45}^0} - {{30}^0}} \right) = \sin {45^0}\cos {30^0} - \cos {45^0}\sin {30^0} = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 3 }}{2} - \frac{{\sqrt 2 }}{2}.\frac{1}{2} = \frac{{\sqrt 6 - \sqrt 2 }}{4}\)
\(\tan {15^0} = \tan \left( {{{45}^0} - {{30}^0}} \right) = \frac{{\tan {{45}^0} - \tan {{30}^0}}}{{1 + \tan {{45}^0}\tan {{30}^0}}} = \frac{{1 - \frac{{\sqrt 3 }}{3}}}{{1 + \frac{{\sqrt 3 }}{3}}} = 2 - \sqrt 3 \)
\(\cot {15^0} = \frac{1}{{\tan {{15}^0}}} = \frac{1}{{2 - \sqrt 3 }}\)

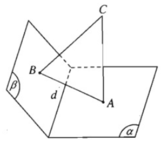
Hai mặt phẳng (α) và (β) không thể trùng nhau vì nếu chúng trùng nhau thì từ một điểm C ta dựng được hai đường thẳng CA, CB cùng vuông góc với một mặt phẳng, điều đó là vô lí.
Mặt khác (α) và (β) cũng không song song với nhau.
Vì nếu (α) // (β), thì từ CB ⊥ (β) ta suy ra CB ⊥ (α)
Như vậy từ một điểm C ta dựng được hai đường thẳng CA, CB cùng vuông góc với (α), điều đó là vô lí.
Vậy (α) và (β) là hai mặt phẳng không trùng nhau, không song song với nhau và chúng phải cắt nhau theo giao tuyến d, nghĩa là d = (α) ∩ (β)
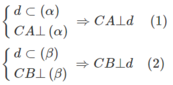
Từ (1) và (2) suy ra d ⊥ (ABC).

Ta có:
\(\begin{array}{l}\cos \alpha \cos \beta = \cos \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right) + \cos \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \alpha + \cos \beta } \right)\end{array}\)
\(\begin{array}{l}\sin \alpha \sin \beta = \sin \frac{{\alpha + \beta }}{2}\sin \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right) - \cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \beta - \cos \alpha } \right)\end{array}\)
\(\begin{array}{l}\sin \alpha \cos \beta = \sin \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\sin \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right) + \sin \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\sin \alpha + \sin \beta } \right)\end{array}\)

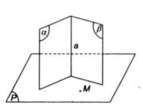

Vậy (MHK) chính là mặt phẳng đi qua M và vuông góc với (α) và (β).
Kết quả: Mặt phẳng (P) cần dựng (tức mp(MHK)) là mặt phẳng đi qua M và vuông góc với Δ.
Vì qua một điểm chỉ có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước nên (P) là duy nhất.
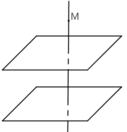
Nếu (α) // (β) thì qua M ta chỉ có thể vẽ một đường thẳng Δ vuông góc với (α) và (β). Bất kì mặt phẳng (P) nào chứa Δ cũng đều vuông góc với (α), (β). Trường hợp này, qua M có vô số mặt phẳng vuông góc với (α), (β).
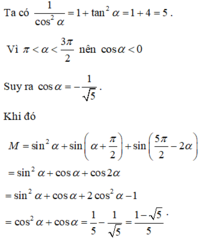
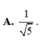
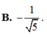
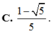
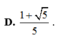

\(\begin{array}{l}\cos \left( {\alpha + \alpha } \right) = \cos 2\alpha = \cos \alpha \cos \alpha - \sin \alpha sin\alpha = {\cos ^2}\alpha - {\sin ^2}\alpha \\ = {\cos ^2}\alpha + {\sin ^2}\alpha - 2{\sin ^2}\alpha = 1 - 2{\sin ^2}\alpha = 2{\cos ^2}a - 1\end{array}\)
\(\tan 2\alpha = \tan \left( {\alpha + \alpha } \right) = \frac{{\tan \alpha + \tan \alpha }}{{1 - \tan \alpha .\tan \alpha }} = \frac{{2\tan a}}{{1 - {{\tan }^2}a}}\)