Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\left(OA,OM\right)=120^o+k\cdot360^o,k\in Z\\ \left(OA,ON\right)=-75^o+k\cdot360^o,k\in Z\)

Công thức tổng quát số đo của góc lượng giác \(\left(Ox,ON\right)=70^o+k\cdot360,k\in Z\)
Công thức tổng quát số đo của lượng giác
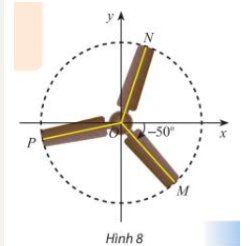
\(\left(Ox,OP\right)=\left(Ox,OM\right)+\left(OM,OP\right)=-50-120^o+m\cdot360^o=-170^o+m\cdot360^o,m\in Z\)

a) Ta có:
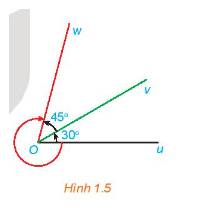
- Các góc lượng giác tia đầu Ou, tia cuối Ov có số đo là
sđ\((Ou,Ov) = {30^ \circ } + n{.360^ \circ }\)
- Các góc lượng giác tia đầu Ov, tia cuối Ow có số đo là
sđ \((Ov,Ow) = {45^ \circ } + m{.360^ \circ }\)
- Các góc lượng giác tia đầu Ou, tia cuối Ow có số đo là
sđ \((Ou,Ow) = {75^ \circ } + k{.360^ \circ }\)
b) Với các góc lượng giác ở câu a, ta có:
\(sđ(Ou,Ov) +sđ (Ov,Ow)\)
\( = {30^ \circ } + n{.360^ \circ } + {45^ \circ } + m{.360^ \circ } \)
\(= {75^ \circ } + (n+m){.360^ \circ } \)
\(= {75^ \circ } + k{.360^ \circ = sđ (Ou,Ow)} \)
với k = n + m

Vì mâm bánh xe ô tô được chia thành năm phần bằng nhau nên mỗi phần có số đo bằng \(\dfrac{360^o}{5}=72^o\)
Ta có: \(\left(ON,OM\right)=\left(ON,Ox\right)+\left(Ox,OM\right)\\ \Rightarrow\left(ON,Ox\right)=99^o\)
Công thức số đo tổng quát của góc lượng giác \(\left(ON,Ox\right)=99^o+k\cdot360^o,k\in Z\)

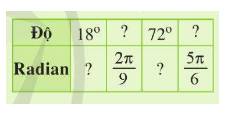
Ta có bảng chuyển đổi số đo độ và số đo radian của một số góc sau:
Độ | \({18^ \circ }\) | \(\frac{{2\pi }}{9}.\frac{{180}}{\pi } = {40^ \circ }\) | \({72^ \circ }\) | \(\frac{{5\pi }}{6}.\frac{{180}}{\pi } = {150^ \circ }\) |
Radian | \(18.\frac{\pi }{{180}} = \frac{\pi }{{10}}\) | \(\frac{{2\pi }}{9}\) | \(72.\frac{\pi }{{180}} = \frac{{2\pi }}{5}\) | \(\frac{{5\pi }}{6}\) |

Tham khảo:
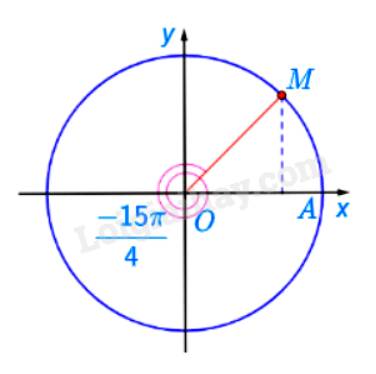
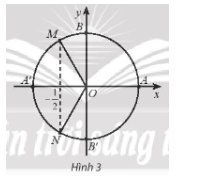
Điểm biểu diễn góc lượng giác có số đo bằng \( - \frac{{15\pi }}{4} = - \frac{{7\pi }}{4} + ( - 1).2\pi \) được xác định là điểm M.
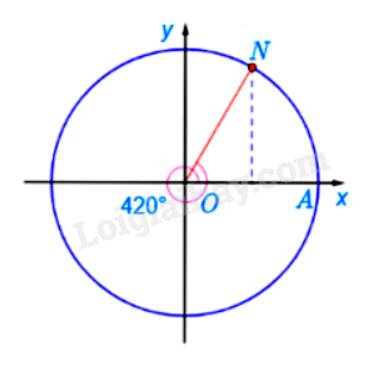
Ta có \(\frac{{420}}{{360}} = 1+ \frac{1}{6}\) Ta chia đường tròn thành 6 phần bằng nhau. Khi đó điểm N là điểm biểu diễn bởi góc có số đo \({420^ \circ }\)

Điểm biểu diễn góc lượng giác x có \(cosx = \frac{{ - 1}}{2}\) là M và N.
Số đo góc lượng giác có điểm biểu diễn M là: \(\frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}\).
Số đo góc lượng giác có điểm biểu diễn N là: \(\frac{{4\pi }}{3} + k2\pi ,k \in \mathbb{Z}\).

a)
x | \( - \pi \) | \( - \frac{{2\pi }}{3}\) | \[ - \frac{\pi }{2}\] | \( - \frac{\pi }{3}\) | 0 | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\pi \) |
\(y = \cos x\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 | \( - \frac{1}{2}\) | -1
|
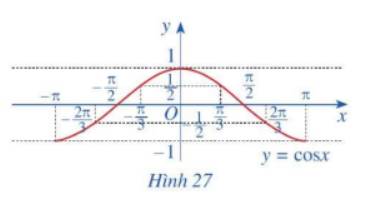
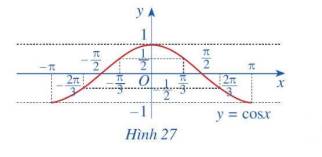
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
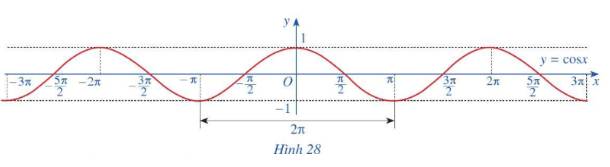
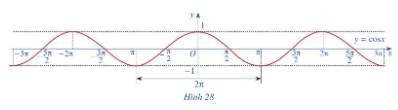
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.
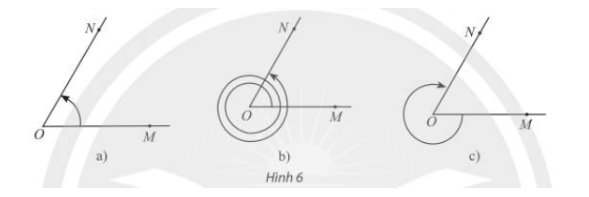



a, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(60^o\)
b, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(60^o+2\cdot360^o=780^o\)
c, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(\dfrac{5}{6}\cdot\left(-360^o\right)=-300^o\)
Công thức tổng quát của số đo góc lượng giác (OM, ON) \(=60^o+360^o\cdot k,k\in Z\)