Cho tam giác ABC ( ∠ A = 90 0 ) có đường cao AH. Chứng minh rằng A H 2 = B H . C H
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 5 2021
a, Xét \(\Delta AEB\)và \(\Delta AFC\)có :
\(+,\widehat{A}\)chung
\(+,AB=AC\)( \(\Delta ABC\)cân tại A )
\(+,\widehat{ABE}=\widehat{ACE}\left(\widehat{AEB}=\widehat{AFC}=90^0\right)\)
\(\Rightarrow\Delta AEB=\Delta AFC\)
b, \(\Delta AEB=\Delta AFC\left(cmt\right)\)
\(\Rightarrow AF=AE\)
Xét \(\Delta AEH\)và \(\Delta AFH\)có :
\(+,\widehat{AFH}=\widehat{AEH}=90^0\)
\(+,AF=AE\) \(\hept{\begin{cases}\\\Rightarrow\Delta AFH=\Delta\\\end{cases}AEH\left(c.c.c\right)}\)
\(+,AH\)chung
\(\Rightarrow\widehat{FAH}=\widehat{AEH}\)
\(\Rightarrow\)AH là tia phân giác của của góc \(\widehat{A}\)
Mặt khác \(\Delta ABC\)cân tại A
\(\Rightarrow AH\perp BC\)
c, Tự làm nhé ..
CM
26 tháng 12 2017
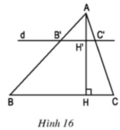
a) Theo hệ quả định lý Ta let ta có:
ΔABC có B’C’ // BC (B’ ∈ AB; C’ ∈ AC) ⇒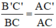 
ΔAHC có H’C’ // HC (H’ ∈ AH, C’ ∈ AC) ⇒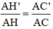 
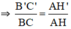
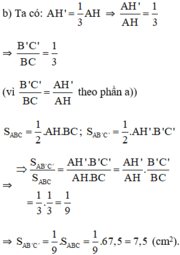
10 tháng 5 2022
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
Do đó: ΔABC\(\sim\)ΔHAC
b: Ta có: ΔABC\(\sim\)ΔHAC
nên AC/HC=BC/AC
hay \(AC^2=BC\cdot HC\)
c: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
10 tháng 5 2022
a, Xét Δ ABC và Δ HAC, có :
\(\widehat{ACB}=\widehat{HCA}\) (góc chung)
\(\widehat{BAC}=\widehat{AHC}=90^o\)
=> Δ ABC ∾ Δ HAC (g.g)
b, Ta có : Δ ABC ∾ Δ HAC (cmt)
=> \(\dfrac{AC}{HC}=\dfrac{BC}{AC}\)
=> \(AC^2=BC.HC\)
c, Xét Δ ABC, có :
\(BC^2=AB^2+AC^2\) (định lí Py - ta - go)
=> \(BC^2=3^2+4^2\)
=> \(BC^2=25\)
=> \(BC=5\left(cm\right)\)
H9
HT.Phong (9A5)
CTVHS
17 tháng 10 2023
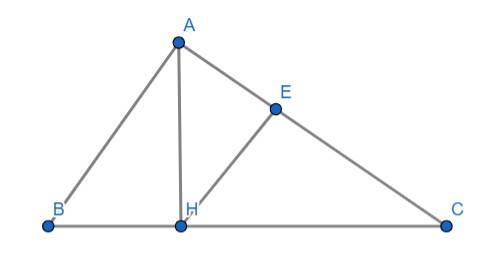
Ta có:
\(\left\{{}\begin{matrix}AB^2=BC\cdot BH\Rightarrow AB=\sqrt{BC\cdot BH}=\sqrt{\left(8+2\right)\cdot2}=2\sqrt{5}\left(cm\right)\\AC^2=BC\cdot CH\Rightarrow AC=\sqrt{BC\cdot CH}=\sqrt{\left(8+2\right)\cdot8}=4\sqrt{5}\left(cn\right)\end{matrix}\right.\)
\(BC\cdot AH=AB\cdot AC\)
\(\Rightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{2\sqrt{5}\cdot4\sqrt{5}}{2+8}=4\left(cm\right)\)
\(sinC=\dfrac{AB}{BC}=\dfrac{2\sqrt{5}}{10}\Rightarrow\widehat{C}\approx27^o\)
SG
2
NA
12 tháng 5 2017
xét tam giác AHB và tam giác CHA có
góc H = 90 độ
AH là cạnh chung
góc B = góc C (kề bù)
suy ra tam giác AHB đồng dạng tam giác CHA( G.C.G)
\(\dfrac{AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH\cdot AH=HB\cdot HC\)
\(\Rightarrow AH^2=HB\cdot HC\)
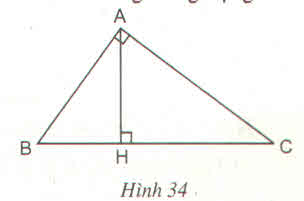
Xét hai tam giác vuông HBA và HAC, ta có:
∠ (AHB) = ∠ (AHC) = 90 0
∠ B = ∠ (HAC) (hai góc cùng phụ C )
Suy ra: △ HBA đồng dạng △ HAC (g.g)
Suy ra: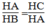
Vậy A H 2 = B H . C H