Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét tam giác AHB và tam giác CHA có
góc H = 90 độ
AH là cạnh chung
góc B = góc C (kề bù)
suy ra tam giác AHB đồng dạng tam giác CHA( G.C.G)
\(\dfrac{AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH\cdot AH=HB\cdot HC\)
\(\Rightarrow AH^2=HB\cdot HC\)

A B C H
a) Xét tam giác HBA và tam giác ABC :
\(\widehat{AHB}=\widehat{BAC}\left(=90^0\right)\)
\(\widehat{ABC}\)chung
=> tam giác HBA \(~\)tam giác ABC ( đpcm )
b) Chứng minh tương tự câu a) ta có tam giác ABC \(~\)tam giác HAC
\(\Rightarrow\frac{AC}{HC}=\frac{BC}{AC}\)
\(\Rightarrow AC^2=HC\cdot BC\)( đpcm )
c) Áp dụng đính lý Pytago vào tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=\sqrt{15^2+20^2}=25\)( cm )
Từ câu b) ta có : \(HC=\frac{AC^2}{BC}=\frac{20^2}{25}=16\)
Vậy....

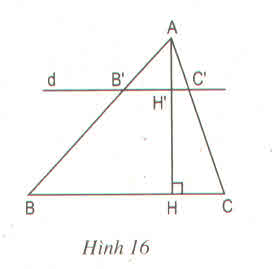
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = 1313 AH
B′C′BCB′C′BC = AH′AHAH′AH = 1313 => B'C' = 1313 BC
=> SAB’C’= 1212 AH'.B'C' = 1212.1313AH.1313
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = 1313 AH
B′C′BCB′C′BC = AH′AHAH′AH = 1313 => B'C' = 1313 BC
=> SAB’C’= 1212 AH'.B'C' = 1212.1313AH.1313BC
=>SAB’C’= (1212AH.BC)1919
mà SABC= 1212AH.BC = 67,5 cm2
Vậy SAB’C’= 1919.67,5= 7,5 cm2

\(\frac{AH}{BH}=\frac{CH}{AH}\Rightarrow AH^2=BH.CH\)
giả sử tam giác ABC vuôgn tại A, AH là đường cao => \(AH^2=BH.CH\)
=> thỏa mãn đk đầu bài => điều gs đúng => tam giác ABC vuôgn tại A
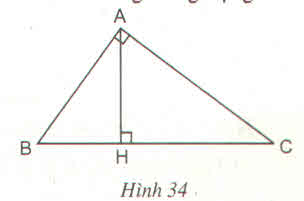




Xét hai tam giác vuông HBA và HAC, ta có:
∠ (AHB) = ∠ (AHC) = 90 0
∠ B = ∠ (HAC) (hai góc cùng phụ C )
Suy ra: △ HBA đồng dạng △ HAC (g.g)
Suy ra: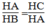
Vậy A H 2 = B H . C H