Cho hình vẽ, biết \(\widehat{xMQ}=60^0\), \(\widehat{MQN}=40^0\) , \(\widehat{yNQ}=100^0\) . Chứng tỏ rằng Mx // Ny.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

giải
a) Vì góc aOb là góc bẹt nên:
\(\widehat{aOm}+\widehat{bOm}=180^0\)
\(\Rightarrow\widehat{bOm}=180^0-\widehat{aOm}=180^0-100^0=80^0\)
b) Vì \(\widehat{bOn}=40^0;\widehat{bOm}=80^0\) nên \(\widehat{bOn}< \widehat{bOm}\left(40^0< 80^0\right)\)
Do đó On nằm giữa hai tia Om và Ob : (1)
\(\widehat{bOn}+\widehat{nOm}=\widehat{bOm}\)
\(\Rightarrow\widehat{nOm}=\widehat{bOm}-\widehat{bOn}=80^0-40^0=40^0\)
\(\Rightarrow\widehat{bOn}=\widehat{nOm}\left(=40^0\right)\) (2)
Từ (1) và (2) suy ra On là tia phân giác \(\widehat{bOm}\)
Vẽ hình ko chính xác mấy, thông cảm nhé!

Câu 1
a.
Xét \(\Delta ABC\) có :
\(\widehat{ABC}+\widehat{BAC}+\widehat{BCA}=180^o\) ( định lý tổng 3 góc của 1 \(\Delta\) )
\(\Rightarrow\widehat{BCA}=40^o\) (1)
Ta có Ax là tia đối của AB
suy ra \(\widehat{BAC}+\widehat{CAx}=180^o\)
\(\widehat{CAx}=80^o\)
lại có Ay là tia phân giác \(\widehat{CAx}\)
\(\Rightarrow\widehat{xAy}=\widehat{yAc}=\dfrac{\widehat{CAx}}{2}=\dfrac{80^o}{2}=40^o\) (2)
Từ (1)(2) suy ra \(\widehat{yAc}=\widehat{ACB}=40^o\)
mà chúng ở vị trí so le trong
\(\Rightarrow\) Ay//BC
Bài 2
Rảnh làm sau , đến giờ học rồi .

Giải:
Do AB // CD nên: \(\widehat{AMN}+\widehat{MNC}=180^o\) ( 2 góc trong cùng phía bù nhau )
\(\Rightarrow\widehat{AMx}+\widehat{xMN}+\widehat{MNC}=180^o\)
Do \(\widehat{AMx}=\widehat{CNy}\left(gt\right)\)
\(\Rightarrow\widehat{CNy}+\widehat{xMN}+\widehat{MNC}=180^o\)
\(\Rightarrow\left(\widehat{CNy}+\widehat{MNC}\right)+\widehat{xMN}=180^o\)
\(\Rightarrow\widehat{MNy}+\widehat{xMN}=180^o\)
Mà 2 góc \(\widehat{MNy},\widehat{xMN}\) ở vị trí trong cùng phía
\(\Rightarrow\)Mx // Ny ( đpcm )
Vậy...

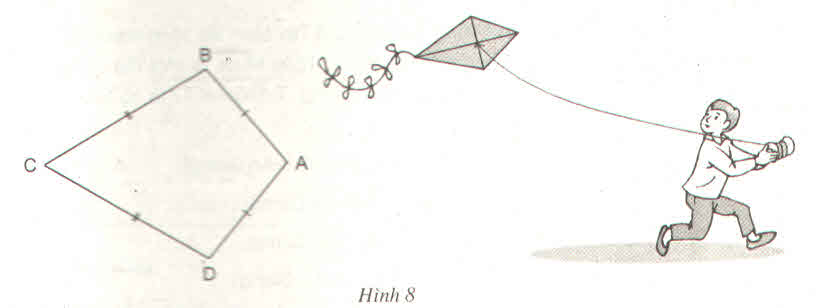
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)

Suy ra: ⇒ \(\widehat{B}=\widehat{D}\)
Ta có \(\widehat{B}+\widehat{D}=360^o-\left(100^o+60^o\right)=200^o\)
Do đó \(\widehat{B}=\widehat{D}=100^o\)
Bài giải:
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)

Suy ra:
Ta có
Do đó

Gọi giao điểm của đường thẳng yN và MQ là A
Vì góc yNQ là góc ngoài tại N của tam giác NAQ
\(\Rightarrow\widehat{yNQ}=\widehat{NQA}+\widehat{NAQ}\Rightarrow\widehat{NAQ}=\widehat{yNQ}-\widehat{NQA}=100-40=60\)
Khi đó \(\widehat{yAQ}=\widehat{xMQ}=60\)ở vị trí đồng vị => xM//yN
Từ Q kẻ đường thẳng Qz về phía x // Mx ta có
^MQz = 180 - ^xMQ = 180-60=120 (hai góc trong cùng phía bù nhau)
=> ^NQz = ^MQz - ^MQN = 120-40=80
Ta có ^yNQ + ^NQz = 100+80=180 => Ny//Qz (Hai đường thẳng bị cắt bởi 1 cát tuyến tạo thành hai góc trong cùng phía bù nhau thì chúng // với nhau)
Mà Qz//Mx
=> Mx//Ny (cùng //Qz)