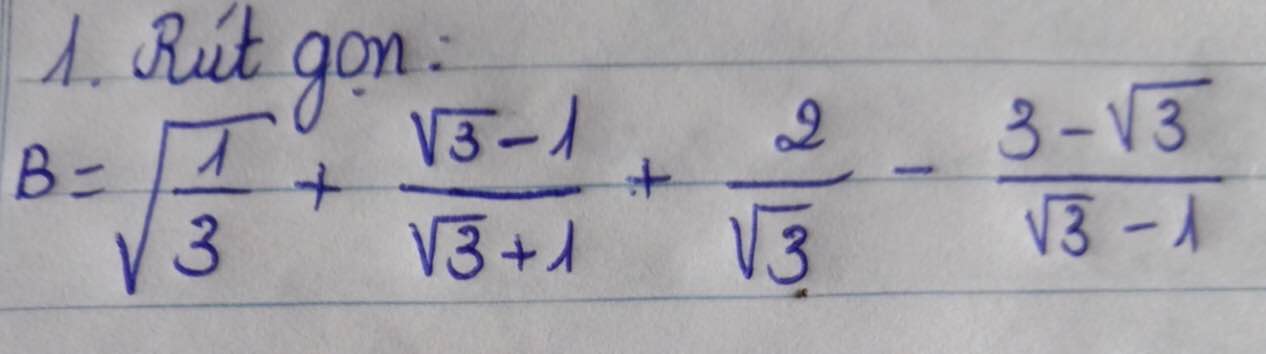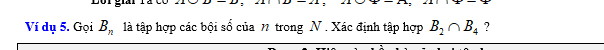Giúp em làm câu 10 với dễ hiểu đi ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
\(y'=\left(x^3\right)'-\left(4x^2\right)'+\left(1\right)'=3x^2-8x\)
Hệ số góc của tiếp tuyến tại điểm có hoành độ bằng 1 là \(y'\left(1\right)\)
\(y'\left(1\right)=3.1^2-8.1=-5\)
10 tháng 10 2021
\(B=\sqrt{\dfrac{1}{3}}+\dfrac{\sqrt{3}-1}{\sqrt{3}+1}+\dfrac{2}{\sqrt{3}}-\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)
\(\Rightarrow B=\dfrac{\sqrt{1}}{\sqrt{3}}+\dfrac{\left(\sqrt{3}-1\right)^2}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}+\dfrac{2}{\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
\(\Rightarrow B=\left(\dfrac{1}{\sqrt{3}}+\dfrac{2}{\sqrt{3}}\right)+\dfrac{3-2\sqrt{3}+1}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}-\sqrt{3}\)
\(\Rightarrow B=\dfrac{3}{\sqrt{3}}+\dfrac{4-2\sqrt{3}}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}-\sqrt{3}\)
\(\Rightarrow B=\sqrt{3}+\dfrac{4-2\sqrt{3}}{\sqrt{3^2}-1^2}-\sqrt{3}\)
\(\Rightarrow B=\dfrac{4-2\sqrt{3}}{2}\)
\(\Rightarrow B=2-\sqrt{3}\)
HN
10 tháng 10 2021
⇔ \(B=\dfrac{1}{\sqrt{3}}+\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}+\dfrac{2}{\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
⇔ \(B=\dfrac{\text{3}}{\sqrt{3}}+\dfrac{3-2\sqrt{3}+1}{3-1}-\sqrt{3}\)
⇔ \(B=\sqrt{3}+\dfrac{\text{4}-2\sqrt{3}}{\text{2}}-\sqrt{3}\)
⇔ \(B=\dfrac{2\left(2-\sqrt{3}\right)}{2}=2-\sqrt{3}\)
TM
0
TT
2
3 tháng 11 2021
\(a,ĐK:-3x\ge0\Leftrightarrow x\le0\left(-3< 0\right)\\ b,ĐK:4-2x\ge0\Leftrightarrow-2x\ge-4\Leftrightarrow x\le2\\ c,ĐK:\dfrac{1}{2x-5}\ge0\Leftrightarrow2x-5>0\left(1>0;2x-5\ne0\right)\\ \Leftrightarrow x>\dfrac{5}{2}\\ d,ĐK:\dfrac{4x+7}{-3}\ge0\Leftrightarrow4x+7\le0\left(-3< 0\right)\Leftrightarrow x\le-\dfrac{7}{4}\)
16 tháng 12 2021
Bải giải :
Ta có : 5260 : 36 = 146 ( dư 4)
Vậy 5260 nan hoa có thể lắp vào 146 xe đạp 2 bánh và còn thừa 4 nan hoa.
Đ/s : 146 xe đạp 2 bánh và còn thừa 4 nan hoa.
Hok tốt
HT
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
\(B_2=\left\{x;x=2k,k\in N\right\}\)
\(B_4=\left\{x;x=4m,m\in N\right\}\)
Do \(4m=2.\left(2m\right)\Rightarrow B_4\subset B_2\)
\(\Rightarrow B_2\cap B_4=B_4\)
NV
5
TB
0
NA
1
12 tháng 10 2021
a: \(\sqrt{252}+\dfrac{1}{3}\sqrt{63}-\sqrt{175}\)
\(=4\sqrt{7}+\sqrt{7}-5\sqrt{7}\)
=0