Tìm tất cả các giá trị thực của tham số m để hàm số y=-x2 +(m-1)x+2 nghịch biến trên khoảng (1;2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 12 2019
Đáp án B
Phương pháp:
Hàm số y = f(x) nghịch biến trên (-∞;+∞) khi và chỉ khi f'(x) ≤ 0, ∀ x ∈ (-∞;+∞), f'(x) = 0 tại hữu hạn điểm.
Cách giải:
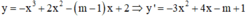
Hàm số đã cho nghịch biến trên khoảng (-∞;+∞)
CM
1 tháng 12 2017
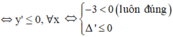
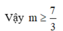
Chọn D.
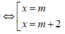
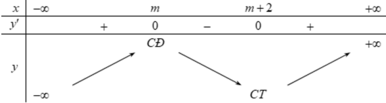
Do đó ta có bảng biến thiên sau:
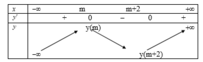
Để hàm số nghịch biến trên khoảng (-1;1) thì
CM
8 tháng 4 2018
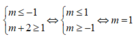
Chọn B.
Tập xác định 
Có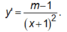 
Hàm số nghịch bến trên mỗi khoảng của tập xác định
CM
30 tháng 9 2018
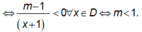
Đáp án A.
Tập xác định: D = ℝ \ − m . Ta có y ' = m 2 − 4 x + m 2 .
Để hàm số nghịch biến trên khoảng − ∞ ; 1 thì ta phải có
m 2 − 4 < 0 1 ≤ − m ⇔ − 2 < m < 2 m ≤ − 1 ⇔ − 2 < m ≤ − 1
Lưu ý: Với cách cho đáp án như trong câu hỏi này, ta có làm như sau:
- Thử với m = − 2 . Khi đó y = − 2 x + 4 x − 2 = − 2 x − 2 x − 2 = − 2 . Suy ra với m = − 2 thì hàm số không nghịch biến trên − ∞ ; 1 . Từ đó loại được đáp án B và C.
- Thử với m = − 1 . Khi đó y = − x + 4 x − 1 . Ta có y ' = − 3 x − 1 2 < 0 ∀ x ≠ 1 .
Suy ra hàm số nghịch biến trên các khoảng − ∞ ; 1 và 1 ; + ∞ . Vậy A là đáp án đúng.
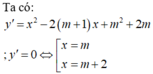
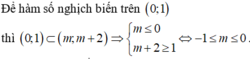
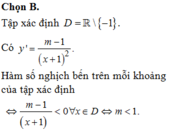
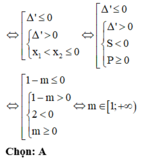
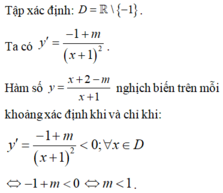
\(a=-1< 0\) ; \(-\frac{b}{2a}=\frac{m-1}{2}\)
\(\Rightarrow\)Hàm số nghịch biến trên \(\left(\frac{m-1}{2};+\infty\right)\)
Để hàm số nghịch biến trên (1;2) thì:
\(\frac{m-1}{2}\le1\Rightarrow m\le3\)