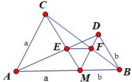
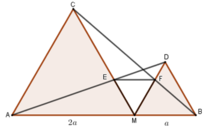
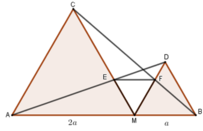
Bài 8: Cho đoạn thẳng AB, M thuộc đoạn thẳng AB. Vẽ về một phía của AB các tam giác đều AMC và BMD, AD giao MC tại E, BC giao MD tại F. Chứng minh:
a) Cho MA=a, MB=b. Tính ME, MF theo a,b
b) Tam giác MEF là tam giác gì?
Bài 9: Cho hình thang ABCD (AB//CD), E là trung điểm của AB, AC giao BD tại O, EO giao CD tại F. Chứng minh:
F là trung điểm của CD


1.
a) + ME // BD
\(\Rightarrow\dfrac{ME}{BD}=\dfrac{AM}{AB}=\dfrac{a}{a+b}\)
\(\Rightarrow\dfrac{ME}{b}=\dfrac{a}{a+b}\Rightarrow ME=\dfrac{ab}{a+b}\)
+ Tương tự : \(MF=\dfrac{ab}{a+b}\)
b) +ΔMEF có ME = MF, \(\widehat{EMF}=60^o\)
=> ΔMEF đều
2.
+ AB // CD \(\Rightarrow\dfrac{AE}{CF}=\dfrac{OE}{OF}\)
+ Tương tự : \(\dfrac{BE}{DF}=\dfrac{OE}{OF}\)
\(\Rightarrow\dfrac{BE}{DF}=\dfrac{AE}{CF}\) => DF = CF ( do AE = BE )
=> F là trung điểm của CD