Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

7)
a) ta có:
\(\widehat{AKE}=\widehat{BAD}\) (đồng vị và AD//KM)
\(\widehat{AEK}=\widehat{DAE}\) (so le trong và AD//KM)
\(\widehat{BAD}=\widehat{DAE}\) (AD là tia phân giác)
=> \(\widehat{AKE}=\widehat{AEK}\)
=> tam giác AKE cân tại A
=> AK=AE
b) Xét tam giác BKM ta có:
AD//KM(gt)
=> \(\dfrac{BK}{AK}=\dfrac{MB}{MD}\) (Đlý thales thuận)
Xét tam giác ADC ta có:
AD//EM(gt)
=> \(\dfrac{CE}{AE}=\dfrac{CM}{MD}\) (Đlý thales thuận)
Mà AE=AK(cmt)
CM=MB(M là trung điểm BC)
Nên \(\dfrac{CE}{AK}=\dfrac{MB}{MD}\)
Mà \(\dfrac{BK}{AK}=\dfrac{MB}{MD}\) (cmt)
Nên CE=AB
9) Xét tam giác ODF ta có:
DF//EB(tc hthang ABCD)
=> \(\dfrac{DF}{EB}=\dfrac{FO}{EO}\) (Hệ quả Thales)
Xét tam giác OCF ta có:
CF//EA(tc hthang ABCD)
=> \(\dfrac{FC}{AE}=\dfrac{FO}{EO}\) (Hệ quả Thales)
Mà \(\dfrac{DF}{EB}=\dfrac{FO}{EO}\) (cmt)
AE=EB(E là trung điểm AB)
Nên DF=FC
=> F là trung điểm DC

a) Ta có:
\(\widehat{CMA}=\widehat{DBA}\left(=60^o\right)\)
Mà 2 góc nằm ở vị trí đồng vị
=> EM//BD
Xét tam giác ABD ta có:
EM//BD(cmt)
=> \(\dfrac{EM}{BD}=\dfrac{AM}{AB}\Rightarrow\dfrac{EM}{b}=\dfrac{a}{ab}\Rightarrow EM=1\)
Cmtt: \(\dfrac{FM}{AC}=\dfrac{BM}{AB}\Rightarrow\dfrac{FM}{b}=\dfrac{a}{ab}\Rightarrow FM=1\)
b) Ta có:
FM=EM(=1)
=> tam giác EMF cân tại M
Ta có:
\(\widehat{CMA}+\widehat{EMF}+\widehat{DMB}=180^o\)
\(60^o+\widehat{EMF}+60^o=180^o\)
\(\widehat{EMF}=60^o\)
Xét tam giác EMF cân tại M ta có:
\(\widehat{EMF}=60^o\) (cmt)
=> tam giác EMF đều

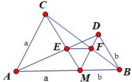
Vì các tam giác AMC và BMD đều nên B M D ^ = M A C ^ = 90 ° (vì hai góc ở vị trí đồng vị) => MD // AC
Vì MD // AC nên theo hệ quả định lý Talet cho hai tam giác DEM và AEC ta có M E E C = M D A C = b a
Suy ra
M E E C = b a ⇒ M E M E + E C = b b + a ⇒ M E a = b b + a ⇒ M E = a b b + a
Tương tự MF = b a a + b
Vậy M E = M F = a b b + a
Đáp án: B

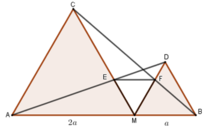
Đặt MB = a => MA = 2a
Vì các tam giác AMC và BMD đều nên B M D ^ = M A C ^ = 60 ° (hai góc ở vị trí đồng vị) => MD // AC
Vì MD // AC nên theo hệ quả định lý Talet cho hai tam giác DEM và AEC ta có
M E E C = M D A C = M B M A = 1 2
Suy ra:
M E E C = b a ⇒ M E M E + E C = 1 1 + 2 = 1 3 ⇒ M E 2 a = 1 3 ⇒ M E = 2 a 3
Tương tự MF = 2 a 3
Vậy M E = M F = 2 a 3
Đáp án: B

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD


a) ABCD là hình thang nên AB//CD
CD=2AB ==>AB/CD=1/2
AB//CD, áp dụng định lý Ta-let, ta có
OA/OC=OB/OD=AB/CD=1/2
=>OA/OC=1/2 => OC=2OA
B) Ta có : OA/OC=OB/OD=AB/CD=1/2
==> OD/OB = 2 ==>OD = 2OB
*xét: OC/AC = 2OA/(OA + OC) = 2OA/(OA + 2OA) = 2OA/3OA = 2/3(1);
OD/BD = 2OB/(OD + OB) = 2OB/(2OB + OB) = 2/3(2)
*từ (1),(2) =>OC/AC = OD/BD = 2/3
=>O là trọng tâm tam giác FCD
c)
Vì một đường thẳng song song với AB và CD lần lượt cắt các đoạn thẳng AD, BD,AC và BC tại M, I,K và N nên KN//AB ,IM//AB và IN//AB
MI//AB, áp dụng hệ quả của định lý Ta-let, ta có
MI/AB = DM/AD = DI/IB (1)
IN//AB, áp dụng định lý Ta-let, ta có
CN/BC=DI/IB (2)
Từ (1) và (2), ta có
DM/AD=CN/BC
d)
KN//AB, áp dụng hệ quả của định lý Ta-let, ta có
KN/AB=CN/BC
Ta có :KN/AB=CN/BC và MI/AB=DM/AD
mà DM/AD=CN/BC nên KN/AB=MI/AB => KN=MI
1.
a) + ME // BD
\(\Rightarrow\dfrac{ME}{BD}=\dfrac{AM}{AB}=\dfrac{a}{a+b}\)
\(\Rightarrow\dfrac{ME}{b}=\dfrac{a}{a+b}\Rightarrow ME=\dfrac{ab}{a+b}\)
+ Tương tự : \(MF=\dfrac{ab}{a+b}\)
b) +ΔMEF có ME = MF, \(\widehat{EMF}=60^o\)
=> ΔMEF đều
2.
+ AB // CD \(\Rightarrow\dfrac{AE}{CF}=\dfrac{OE}{OF}\)
+ Tương tự : \(\dfrac{BE}{DF}=\dfrac{OE}{OF}\)
\(\Rightarrow\dfrac{BE}{DF}=\dfrac{AE}{CF}\) => DF = CF ( do AE = BE )
=> F là trung điểm của CD