Cho \(\Delta ABC\) nhọn, M thuộc miền trong \(\Delta\)ABC. Vẽ MH\(\perp\)AB, MK\(\perp\)BC, MD\(\perp\)AC. Xác định M để MH^2+MK^2+MD^2 nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 4 2017
a,Xét tam giác ABM=ACM có
góc B = góc C (gt)
BM=MC(gt)
AB=AC(gt)
Vậy tam giác ABM = ACM (C-G-C)
Vì MH vuông với AB,MK vuông góc với AC và tam giác ABC cân
=)góc HMB=góc KMC
b, Xét tam giác HBM và KCM có:
BM=MC(gt)
góc HMB=góc KMC
Vậy tam giác HBM=KCM(cạnh huyền góc nhọn)
=)BH = CK (2 cạnh tưng ứng)
c,
\(\widehat{ABM}=\widehat{ACM}\)
Mà \(90^0-\widehat{ABM}=90^0-\widehat{ACM}\)
\(\Leftrightarrow\widehat{IBM}=\widehat{IMB}\)
Vậy tam giác IBM cân tại I.
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
18 tháng 8 2023
a/
\(BH\perp AC\Rightarrow HF\perp AC;ME\perp AC\) => ME//HF
\(AC\perp AB\Rightarrow EH\perp HF;MF\perp BH\Rightarrow MF\perp HF\) => EH//MF
=> MEHF là hình bình hành (tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh) => ME=HF (cạnh đối hbh)
b/
\(\widehat{BMD}+\widehat{ABC}=90^o\)
\(\widehat{CME}+\widehat{ACB}=90^o\)
\(\widehat{ABC}=\widehat{ACB}\) (góc ở đáy tg cân)
\(\Rightarrow\widehat{BMD}=\widehat{CME}\)
Mà \(\widehat{CME}=\widehat{CBH}\) (góc đồng vị)
\(\Rightarrow\widehat{BMD}=\widehat{CBH}\)
Xét tg vuông DBM và tg vuông FMB có
\(\widehat{BMD}=\widehat{CBH}\)
BM chung
=> tg DBM = tg FMB (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)
c/
Ta có ME = HF (cmt)
tg DBM = tg FMB (cmt) => MD = BF
=> MD+ME=BF+HF=BH không đổi
d/
Từ D dựng đt // AC cắt BC tại N
\(\Rightarrow\widehat{BND}=\widehat{ACB}\) Góc đồng vị)
\(\widehat{ABC}=\widehat{ACB}\)
=> \(\widehat{BND}=\widehat{ABC}\) => tg DBN cân tại D => BD=ND (1)
tg DBM = tg FMB (cmt) => BD=MF (2)
Mà MF = EH (cạnh đối hbh) (3)
Mà EH = KC (4)
Từ (1) (2) (3) (4) => ND = KC
Mà ND//AC => ND//KC
=> DEKN là hbh (Tứ giác có 1 cặp cạnh đối // và bằng nhau là hbh)
Mà DK và NC là hai đường chéo của hbh cắt nhau tại trung điểm mỗi đường => trung điểm của KD nằm trên NC mà NC thuộc BC => trung điểm KD nằm trên BC
21 tháng 8 2023
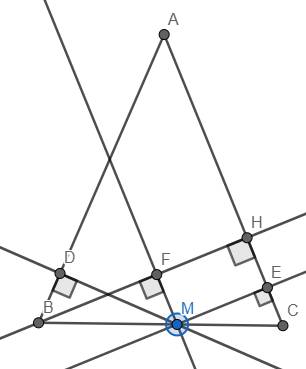
a) Vẽ MH, rõ ràng HEMF có tổng số đo của 4 góc là 360o (vì tổng số đo của 4 góc đó là tổng số đo của các góc của các tam giác FMH và EMH)
Mà theo giả thuyết \(MD\perp AB\), \(ME\perp AC\) và \(MF\perp BH\) nên \(MF\perp ME\). Suy ra HEMF là hình chữ nhật, từ đó ME = HF.
b) Ta có \(\widehat{ABM}=\widehat{ACM}\) (vì tam giác ABC cân tại A) và \(\widehat{FMB}=\widehat{ACM}\) (vì hai góc đồng vị và AC//MF vì \(ME\perp AC\) và \(MF\perp ME\)), suy ra \(\widehat{ABM}=\widehat{FMB}\).
Xét tam giác DBM vuông tại D và FMB vuông tại F có BM là cạnh chung và \(\widehat{ABM}=\widehat{FMB}\), suy ra ΔDBM = ΔFMB (cạnh huyền - góc nhọn)
c) Từ a) và b) suy ra MD = BF, MD + ME = BF + FH = BH. Vậy khi M chạy trên đáy BC thì tổng MD + ME có giá trị không đổi.
VM
11 tháng 11 2019
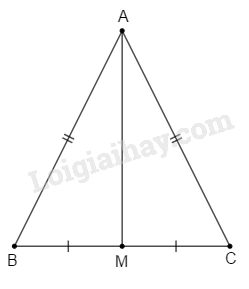
Xét \(\Delta ABC\) có:
c) Ta có \(\Delta ABC\) cân tại \(A\left(cmt\right).\)
=> \(\widehat{B}=\widehat{C}\) (tính chất tam giác cân).
Xét 2 \(\Delta\) vuông \(HBM\) và \(KCM\) có:
\(\widehat{MHB}=\widehat{MKC}=90^0\left(gt\right)\)
\(BM=CM\) (như ở trên)
\(\widehat{B}=\widehat{C}\left(cmt\right)\)
=> \(\Delta HBM=\Delta KCM\) (cạnh huyền - góc nhọn).
=> \(HM=KM\) (2 cạnh tương ứng).
Chúc bạn học tốt!