.Tìm x , biết : a, x + 2 căn x = 0 ; b, 5x= 10 căn x ; 2. Cmr : a, căn 50 - căn 17 > 11 ; b, căn 6 + căn 12 + căn 30 +căn 56 < 19 ; 5. So sánh a, căn 26 + căn 17 và 9 ; b, căn 6 - căn 5 và 1 ; 6. Cho B = căn x +1 tất cả phần căn x - 2 .Tìm x để B nhận giá trị nguyên .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
17 tháng 7 2022
Đúng(0)
Những câu hỏi liên quan
19 tháng 2 2021
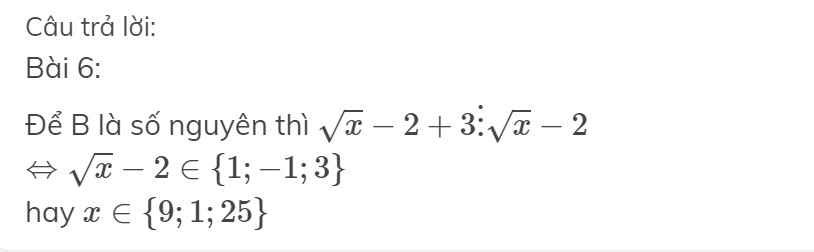
a) Ta có: \(M=\left(\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\right)\cdot\dfrac{x+3\sqrt{x}}{7-\sqrt{x}}\)
\(=\left(\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\right)\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{7-\sqrt{x}}\)
\(=\dfrac{x-9-\left(x-2\sqrt{x}+\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{7-\sqrt{x}}\)
\(=\dfrac{x-9-x+\sqrt{x}+2}{\left(\sqrt{x}-2\right)}\cdot\dfrac{1}{-\left(\sqrt{x}-7\right)}\)
\(=\dfrac{\sqrt{x}-7}{\sqrt{x}-2}\cdot\dfrac{-1}{\sqrt{x}-7}\)
\(=\dfrac{-1}{\sqrt{x}-2}\)(1)
b) Ta có: \(x^2-4x=0\)
\(\Leftrightarrow x\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=4\left(loại\right)\end{matrix}\right.\)
Thay x=0 vào biểu thức (1), ta được:
\(M=\dfrac{-1}{\sqrt{0}-2}=\dfrac{-1}{-2}=\dfrac{1}{2}\)
Vậy: Khi \(x^2-4x=0\) thì \(M=\dfrac{1}{2}\)
DT
Dang Tung
CTVHS
15 tháng 10 2023
\(R=\left(\dfrac{3\sqrt{x}}{\sqrt{x}+2}+\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{3x-5\sqrt{x}}{4-x}\right):\left(\dfrac{2\sqrt{x}-1}{\sqrt{x}-2}-1\right)\left(ĐK:x\ge0,x\ne4\right)\\ =\left(\dfrac{3\sqrt{x}}{\sqrt{x}+2}+\dfrac{\sqrt{x}}{\sqrt{x}-2}+\dfrac{3x-5\sqrt{x}}{\sqrt{x}^2-2^2}\right):\dfrac{2\sqrt{x}-1-\left(\sqrt{x}-2\right)}{\sqrt{x}-2}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)+\sqrt{x}\left(\sqrt{x}+2\right)+3x-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}-2}{2\sqrt{x}-1-\sqrt{x}+2}\\ =\dfrac{3x-6\sqrt{x}+x+2\sqrt{x}+3x-5\sqrt{x}}{\sqrt{x}+2}.\dfrac{1}{\sqrt{x}+1}\)
\(=\dfrac{7x-9\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}\)
Bạn xem lại đề nhé, rút gọn thường ra kết quả rất đẹp chứ không dài như kết quả này đâu ạ.
T
12 tháng 7 2020
cậu cho mk xin link facebook của jonathan galindo đi rồi mk sẽ trả lời câu hỏi của cậu
15 tháng 8 2016
Ta có : \(\frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}=\frac{\left(\sqrt{5}-\sqrt{3}\right)^2}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}=\frac{8-2\sqrt{15}}{2}=4-\sqrt{15}\)
Thay \(x=4-\sqrt{15}\) vào pt được :
\(\left(4-\sqrt{15}\right)^2.a+\left(4-\sqrt{15}\right)b+1=0\Leftrightarrow\left(31-8\sqrt{15}\right)a+\left(4-\sqrt{15}\right)b+1=0\)
\(\Leftrightarrow\sqrt{15}\left(-8a-b\right)+\left(31a+4b+1\right)=0\)
Vì a,b là số hữu tỉ nên ta có : \(\begin{cases}8a+b=0\\31a+4b=-1\end{cases}\) \(\Leftrightarrow\begin{cases}a=1\\b=-8\end{cases}\)
15 tháng 8 2016
Ta có:\(x=\frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}=\frac{\left(\sqrt{5}-\sqrt{3}\right)^2}{5-3}=\frac{8-2\sqrt{15}}{2}=4-\sqrt{15}\)
Thay vào ta có:
\(a\cdot\left(4-\sqrt{15}\right)^2+b\cdot\left(4-\sqrt{15}\right)+1=0\)
\(\Leftrightarrow a\cdot\left(31-8\cdot\sqrt{15}\right)+4b-b\cdot\sqrt{15}+1=0\)
\(\Leftrightarrow\left(31a+4b+1\right)-\left(8a+b\right)\cdot\sqrt{15}=0\)
Do a,b hữu tỉ \(\Rightarrow\begin{cases}31a+4b+1=0\\8a+b=0\end{cases}\)\(\Leftrightarrow\begin{cases}31a-32a+1=0\\b=-8a\left(1\right)\end{cases}\)
31a-3a+1=0 <=>a=1.Từ (1) =>b=-8
Vậy a= 1 và b= -8
NN
1
12 tháng 11 2017
a) \(4x^2-1=0\)
\(\left(2x-1\right)\left(2x+1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}2x-1=0\\2x+1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{1}{2}\\x=\frac{-1}{2}\end{cases}}\)
vậy \(\orbr{\begin{cases}x=\frac{1}{2}\\x=\frac{-1}{2}\end{cases}}\)
b) \(2x^2+0,82=1\)
\(2x^2=1-0,82\)
\(2x^2=0,18\)
\(x^2=\frac{0,18}{2}\)
\(x^2=0,09\)
\(\Rightarrow x=0,3\)
vậy \(x=0,3\)
c) \(7-\sqrt{x}=0\)
\(\sqrt{x}=7\)
\(x=49\)
vậy \(x=49\)
d) ko rõ đề bài
XA
1
AH
Akai Haruma
Giáo viên
29 tháng 10 2023
Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn dễ hơn nhé.