
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


62ab427 chia hết cho 99
=> 62ab427 chia hết cho 9 ;11
Để 62ab427 chia hết cho 11
=> (6+a+4+7)-(2+b+2) chia hết cho 11
=> (17+a)-(4+b) chia hết cho 11
=> 17+a-4-b chia hết cho 11
=> 13+(a-b) chia hết cho 11
Vì -9\(\le\)a-b\(\le\)9
=> a-b= -2;9
Để 62ab427 chia hết cho 9
=> 6+2+a+b+4+2+7 chia hết cho 9
=> 21+a+b chia hết cho 9
=> a+b=6;15
Xét a+b=6 ; a-b= -2
=> a+b-(a-b) = 8
=> 2b=8
=> b=4
=> a= 6-4=2
xét a+b=6; a-b= 9
=> a+b-(a-b) =-3
=> 2b= -3 ( loại vì a;b là số tự nhiên )
Xet a+b= 15 ; a-b= -2
=> (a+b)-(a-b)= 17
=> 2b=17
=> b= 8,5 ( loại vì a;b là số tự nhiên )
Xet a+b=15; a-b=9
=> a+b-(a-b)=6
=> 2b=6
=> b=3
=> a = 12 ( loại vì a;b là các số có 1 chữ số )
Vậy (a;b)= (2;4)

dùng phương pháp dấu hiệu chia hết cho 9 và 11 nha bn
tick tick tick mk muôn tick

\(\overline{1a31b5}\) ⋮ 99
⇒ \(\overline{1a31b5}\) ⋮ 9; 11
\(\overline{1a31b5}\) ⋮ 9 ⇒ 1 + \(a\) + 3 + 1 + \(b\) + 5 ⋮ 9 ⇒ \(a\) + \(b\) + 1 ⋮ 9 (1)
\(\overline{1a31b5}\)⋮11 ⇒ 1 + 3 + \(b\) = \(a\) + 1 + 5 ⇒ \(b\) = \(a\) + 2
Thay \(b=a\) + 2 vào biểu thức (1) ta có:
\(a\) + \(a\) + 2 + 1 ⋮ 9 ⇒ 2\(a\) = 6; 15; 18
Lập bảng ta có:
| 2\(a\) | 6 | 15 | 18 |
| \(a\) | 3 | 7,5(loại) | 9 |
| \(b\) = \(a+2\) | 5 | 11(loại) | |
| \(\overline{1a31b5}\) | 133155 |
Theo bảng trên ta có các chữ số a; b thỏa mãn đề bài là:
\(\left\{{}\begin{matrix}a=3\\b=5\end{matrix}\right.\)

Câu 1 : để 18ab chia hết cho 5 thì b =0 hoặc 5
Nếu b =0 . Ta có 18a0 chia hết cho 8
suy ra 8+a+0 chia hết cho 8
suy ra 8+a chia hết cho 8
suy ra a= 0;8

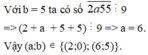
Ta có
99=9.11
9 và 11 là 2 số nguyên tố cùng nhau nên
\(\overline{62ab427}⋮99\) khi \(\overline{62ab427}\) đồng thời chia hết cho 9 và 11
\(\overline{62ab427}⋮9\Rightarrow6+2+a+b+4+2+7=21+\left(a+b\right)⋮9\)
\(\Rightarrow\left(a+b\right)=\left\{6;15\right\}\) (1)
Để 1 số chia hết cho 11 thì hiệu giữa tổng các chữ số ở vị trí chẵn (lẻ) với tổng các chữ số ở vị trí lẻ (chẵn) chia hết cho 11
\(\Rightarrow\overline{62ab427}⋮11\) khi (6+a+4+7)-(2+b+2)=13+(a-b)\(⋮11\)
\(13+\left(a-b\right)=11+a-b+2⋮11\Rightarrow a-b+2⋮11\)
\(\Rightarrow\left(a-b\right)=\left\{-2;9\right\}\) (2)
Từ (1) và (2) ta có các TH
TH1: \(\left\{{}\begin{matrix}a+b=6\\a-b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=4\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}a+b=6\\a-b=9\end{matrix}\right.\) (loại vì a không nguyên)
TH3: \(\left\{{}\begin{matrix}a+b=15\\a-b=-2\end{matrix}\right.\) (loại vì a không nguyên)
TH4: \(\left\{{}\begin{matrix}a+b=15\\a-b=9\end{matrix}\right.\) (loại vì a>9)
\(\Rightarrow\overline{62ab427}=6224427⋮99\)
B=62xy427
B chia hết cho 99 => B chia hết cho 9 và 11
B chia hết cho 9 => x=7 chia 9 dư 6
=> x+y bằng 6 hoặc 15(1)
B chia hết cho 11=> (7+4+x+6)-(2+y+2)= 11k hoặc 13+x-y=11k(2)
Từ (2) suy ra y-x=13-11k . Vì x,y là số tự nhiên nhỏ hơn 10 nên k =1
=> y-x=2(3)
*x+y=6 ; y-x=2 => x=2; y=-4
*x+y=15 ; y-x=2 => vô nghiệm (vì x, y nguyên)
Vậy có 1 đáp án là B = 6224427