K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
\(\dfrac{x-3}{3}=\dfrac{2x+1}{5}\)
`=> (x-3)5 = (2x+1)3`
`=> 5x-15 = 6x+3`
`=> 5x-6x = 15+3`
`=> -x=18`
`=> x=-18`
\(\dfrac{x+1}{22}=\dfrac{6}{x}\)
`=> (x+1)x = 22*6`
`=> (x+1)x = 132`
`=> x^2 + x = 132`
`=> x^2+x-132=0`
`=> (x-11)(x+12)=0`
`=>`\(\left[{}\begin{matrix}x-11=0\\x+12=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=11\\x=-12\end{matrix}\right.\)
\(\dfrac{2x-1}{2}=\dfrac{5}{x}\)
`=> (2x-1)x = 2*5`
`=> 2x^2 - x =10`
`=> 2x^2 - x - 10 =0`
`=> 2x^2 + 4x - 5x - 10 =0`
`=> (2x^2 + 4x) - (5x+10)=0`
`=> 2x(x+2) - 5(x+2)=0`
`=> (2x-5)(x+2)=0`
`=>`\(\left[{}\begin{matrix}2x-5=0\\x+2=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}2x=5\\x=-2\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-2\end{matrix}\right.\)
\(\dfrac{2x-1}{21}=\dfrac{3}{2x+1}\)
`=> (2x-1)(2x+1)=21*3`
`=> 4x^2 + 2x - 2x - 1 = 63`
`=> 4x^2 - 1=63`
`=> 4x^2 - 1 - 63=0`
`=> 4x^2 - 64 = 0`
`=> 4(x^2 - 16)=0`
`=> 4(x^2 + 4x - 4x - 16)=0`
`=> 4[(x^2+4x)-(4x+16)]=0`
`=> 4[x(x+4)-4(x+4)]=0`
`=> 4(x-4)(x+4)=0`
`=>`\(\left[{}\begin{matrix}x-4=0\\x+4=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)
\(\dfrac{2x+1}{9}=\dfrac{5}{x+1}\)
`=> (2x+1)(x+1) = 9*5`
`=> (2x+1)(x+1)=45`
`=> 2x^2 + 2x + x + 1 = 45`
`=> 2x^2 + 3x + 1 =45`
`=> 2x^2 + 3x + 1 - 45 =0`
`=> 2x^2+3x-44=0`
`=> 2x^2 + 11x - 8x - 44=0`
`=> (2x^2 +11x) - (8x+44)=0`
`=> x(2x+11) - 4(2x+11)=0`
`=> (x-4)(2x+11)=0`
`=>`\(\left[{}\begin{matrix}x-4=0\\2x+11=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=4\\2x=-11\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=4\\x=-\dfrac{11}{2}\end{matrix}\right.\)
BD
15 tháng 6 2023
\(\dfrac{x-3}{3}=\dfrac{2x+1}{5}\\ \left(x-3\right)\cdot5=\left(2x+1\right)\cdot3\\ x5-15=6x+3\\ x5-6x=3+15\\ -x=18\\ \Rightarrow x=-18\)
\(\dfrac{x+1}{22}=\dfrac{6}{x}\\ \left(x+1\right)\cdot x=6\cdot22\\ \left(x+1\right)\cdot x=2\cdot3\cdot2\cdot11\\ \left(x+1\right)\cdot x=12\cdot11\\ \Rightarrow x=11\)
\(\dfrac{2x-1}{21}=\dfrac{3}{2x+1}\\ \left(2x-1\right)\cdot\left(2x+1\right)=21\cdot3\\ \left(2x-1\right)\cdot\left(2x+1\right)=7\cdot3\cdot3\\ \left(2x-1\right)\cdot\left(2x+1\right)=7\cdot9\\ \Rightarrow2x+1=9\\ 2x=8\\ x=4\)
S
1
25 tháng 8 2020
a) \(2x+\frac{3}{15}=\frac{7}{5}\)
=> \(2x=\frac{7}{5}-\frac{3}{15}=\frac{21}{15}-\frac{3}{15}=\frac{18}{15}\)
=> \(x=\frac{18}{15}:2=\frac{18}{15}\cdot\frac{1}{2}=\frac{9}{15}\cdot\frac{1}{1}=\frac{9}{15}\)
b) \(x-\frac{2}{9}=\frac{8}{3}\)
=> \(x=\frac{8}{3}+\frac{2}{9}\)
=> \(x=\frac{24}{9}+\frac{2}{9}=\frac{26}{9}\)
c) \(\frac{-8}{x}=\frac{-x}{18}\)
=> x(-x) = (-8).18
=> -x2 = -144
=> x2 = 144(bỏ dấu âm)
=> x = \(\pm\)12
d) \(\frac{2x+3}{6}=\frac{x-2}{5}\)
=> 5(2x + 3) = 6(x - 2)
=> 10x + 15 = 6x - 12
=> 10x + 15 - 6x + 12 = 0
=> 4x + 27 = 0
=> 4x = -27
=> x = -27/4
e) \(\frac{x+1}{22}=\frac{6}{x}\)
=> x(x + 1) = 132
=> x(x + 1) = 11.12
=> x = 11
f) \(\frac{2x-1}{2}=\frac{5}{x}\)
=> x(2x - 1) = 10
=> 2x2 - x = 10
=> 2x2 - x - 10 = 0
tới đây tự làm đi nhé
g) \(\frac{2x-1}{21}=\frac{3}{2x+1}\)
=> (2x - 1)(2x + 1) = 63
=> 4x2 - 1 = 63
=> 4x2 = 64
=> x2 = 16
=> x = \(\pm\)4
h) Tương tự
NC
25 tháng 8 2020
a) \(\frac{2x+3}{15}=\frac{7}{5}\Leftrightarrow10x+15=105\Leftrightarrow10x=90\Rightarrow x=9\)
b) \(\frac{x-2}{9}=\frac{8}{3}\Leftrightarrow3x-6=72\Leftrightarrow3x=78\Rightarrow x=26\)
c) \(\frac{-8}{x}=\frac{-x}{18}\Leftrightarrow x^2=144\Leftrightarrow\orbr{\begin{cases}x=12\\x=-12\end{cases}}\)
d) \(\frac{2x+3}{6}=\frac{x-2}{5}\Leftrightarrow10x+15=12x-12\Leftrightarrow2x=27\Rightarrow x=\frac{27}{2}\)
e) \(\frac{x+1}{22}=\frac{6}{x}\Leftrightarrow x^2+x-132=0\Leftrightarrow\left(x-11\right)\left(x+12\right)=0\Leftrightarrow\orbr{\begin{cases}x=11\\x=-12\end{cases}}\)
f) \(\frac{2x-1}{2}=\frac{5}{x}\Leftrightarrow2x^2-x-10=0\Leftrightarrow\left(x-2\right)\left(2x+5\right)=0\Leftrightarrow\orbr{\begin{cases}x=2\\x=-\frac{5}{2}\end{cases}}\)
g) \(\frac{2x-1}{21}=\frac{3}{2x+1}\Leftrightarrow4x^2=64\Leftrightarrow x^2=16\Rightarrow\orbr{\begin{cases}x=4\\x=-4\end{cases}}\)
h) \(\frac{10x+5}{6}=\frac{5}{x+1}\Leftrightarrow10x^2+15x-25=0\Leftrightarrow5\left(x-1\right)\left(2x+5\right)=0\Leftrightarrow\orbr{\begin{cases}x=1\\x=-\frac{5}{2}\end{cases}}\)
C
28 tháng 6 2017
c) \(\left(3x-1\right).\left(2x+7\right)-\left(x+1\right).\left(6x-5\right)=\left(x+2\right)-\left(x-5\right)\)
\(\Leftrightarrow6x^2+21x-2x-7-\left(6x^2-5x+6x-5\right)=x+2-x+5\)
\(\Leftrightarrow18x-2-7=0\)
\(\Rightarrow x=\dfrac{9}{18}=\dfrac{1}{2}\)
C
28 tháng 6 2017
b) \(2.\left(3x-1\right).\left(2x+5\right)-6.\left(2x-1\right).\left(x+2\right)=1\)
\(\Leftrightarrow\left(6x-2\right).\left(2x+5\right)-\left(12x-6\right).\left(x+2\right)=1\)
\(\Leftrightarrow12x^2+30x-4x-10-\left(12x^2+24x-6x-12\right)=1\)
\(\Leftrightarrow12x^2+26x-10-12x^2-18x +12=1\)
\(\Leftrightarrow8x+2=1\)
\(\Rightarrow x=\dfrac{-1}{8}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 9
Bài 1:
- \(\dfrac{11}{2}x\) + 1 = \(\dfrac{1}{3}x-\dfrac{1}{4}\)
- \(\dfrac{11}{2}\)\(x\) - \(\dfrac{1}{3}\)\(x\) = - \(\dfrac{1}{4}\) - 1
-(\(\dfrac{33}{6}\) + \(\dfrac{2}{6}\))\(x\) = - \(\dfrac{5}{4}\)
- \(\dfrac{35}{6}\)\(x\) = - \(\dfrac{5}{4}\)
\(x=-\dfrac{5}{4}\) : (- \(\dfrac{35}{6}\))
\(x\) = \(\dfrac{3}{14}\)
Vậy \(x=\dfrac{3}{14}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 9
Bài 2: 2\(x\) - \(\dfrac{2}{3}\) - 7\(x\) = \(\dfrac{3}{2}\) - 1
2\(x\) - 7\(x\) = \(\dfrac{3}{2}\) - 1 + \(\dfrac{2}{3}\)
- 5\(x\) = \(\dfrac{9}{6}\) - \(\dfrac{6}{6}\) + \(\dfrac{4}{6}\)
- 5\(x\) = \(\dfrac{7}{6}\)
\(x\) = \(\dfrac{7}{6}\) : (- 5)
\(x\) = - \(\dfrac{7}{30}\)
Vậy \(x=-\dfrac{7}{30}\)
2 tháng 4 2020
1: Ta có: \(2x+x\left(x-5\right)=3x^2-x\)
\(\Leftrightarrow2x+x^2-5x-3x^2+x=0\)
\(\Leftrightarrow-2x^2-2x=0\)
\(\Leftrightarrow-2x\left(x+1\right)=0\)
Vì -2≠0
nên \(\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
Vậy: x∈{0;-1}
2) Ta có: \(15-5\left(1-2x\right)=12-x\)
\(\Leftrightarrow15-5+10x-12+x=0\)
\(\Leftrightarrow11x-2=0\)
\(\Leftrightarrow11x=2\)
hay \(x=\frac{2}{11}\)
Vậy: \(x=\frac{2}{11}\)
3) Ta có: \(\frac{2}{3}-\frac{1}{3}\left(x-\frac{3}{2}\right)-\frac{1}{2}\left(2x+1\right)=5\)
\(\Leftrightarrow\frac{2}{3}-\frac{1}{3}x+\frac{1}{2}-x-\frac{1}{2}-5=0\)
\(\Leftrightarrow\frac{-13}{3}-\frac{4}{3}x=0\)
\(\Leftrightarrow\frac{4}{3}x=\frac{-13}{3}\)
hay \(x=\frac{-13}{3}:\frac{4}{3}=\frac{-13}{4}\)
Vậy: \(x=\frac{-13}{4}\)
4) Ta có: \(\left|x-\frac{4}{5}\right|=\frac{3}{5}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\frac{4}{5}=\frac{3}{5}\\x-\frac{4}{5}=\frac{-3}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{7}{5}\\x=\frac{1}{5}\end{matrix}\right.\)
Vậy: \(x\in\left\{\frac{1}{5};\frac{7}{5}\right\}\)
BL
2 tháng 4 2020
1. \(2x+x\left(x-5\right)=3x^2-x\)
\(\Leftrightarrow2x+x^2-5x=3x^2-x\)
\(\Leftrightarrow\left(2x-5x+x\right)+\left(x^2-3x^2\right)=0\)
\(\Leftrightarrow-2x-2x^2=0\)
\(\Leftrightarrow-2x\left(1+x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\1+x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
2. \(15-5\left(1-2x\right)=12-x\)
\(\Leftrightarrow15-5+10x=12-x\)
\(\Leftrightarrow\left(15-5-12\right)+\left(10x+x\right)=0\)
\(\Leftrightarrow-2+11x=0\)
\(\Leftrightarrow11x=2\Leftrightarrow x=\frac{2}{11}\)
3. \(\frac{2}{3}-\frac{1}{3}\left(x-\frac{3}{2}\right)-\frac{1}{2}\left(2x+1\right)=5\)
\(\Leftrightarrow\frac{2}{3}-\frac{1}{3}x+\frac{1}{2}-x-\frac{1}{2}=5\)
\(\Leftrightarrow\left(\frac{2}{3}+\frac{1}{2}-\frac{1}{2}-5\right)-\left(\frac{1}{3}x+x\right)=0\)
\(\Leftrightarrow-\frac{13}{3}-\frac{4}{3}x=0\)
\(\Leftrightarrow-\frac{4}{3}x=\frac{13}{3}\Leftrightarrow x=-\frac{13}{4}\)
4. \(\left|x-\frac{4}{5}\right|=\frac{3}{5}\)
\(\Rightarrow x-\frac{4}{5}=-\frac{3}{5}\) hoặc \(x-\frac{4}{5}=\frac{3}{5}\)
\(TH1:x-\frac{4}{5}=-\frac{3}{5}\Rightarrow x=\frac{1}{5}\)
\(TH2:x-\frac{4}{5}=\frac{3}{5}\Rightarrow x=\frac{7}{5}\)
DN
1
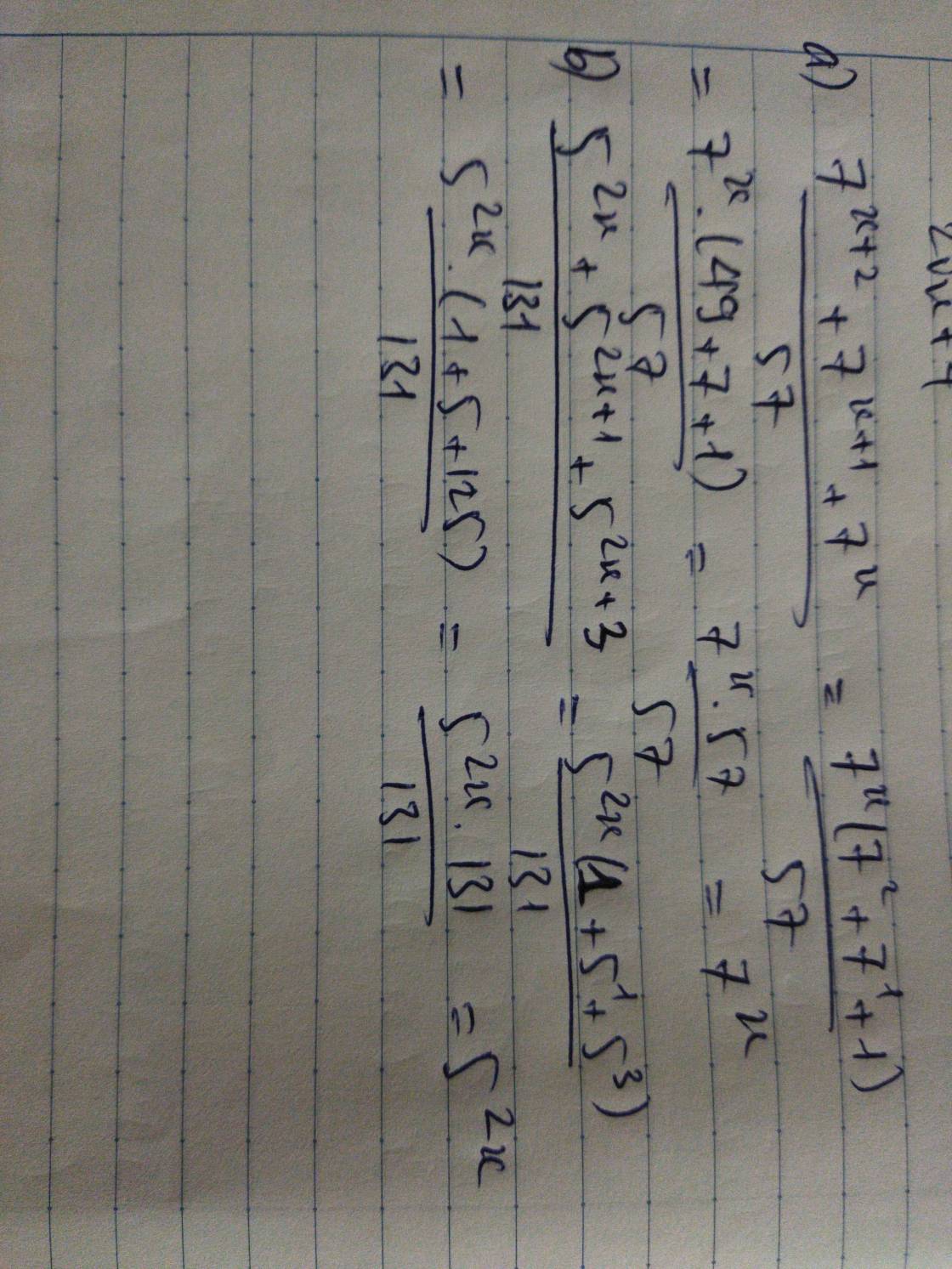
|x-1|=2x-5
x= 4 nha bạn
chúc bạn học tốt
\(\left|x-1\right|=2x-5\)ĐK : x >= 5/2
TH1 : \(x-1=2x-5\Leftrightarrow x=4\)(tm)
TH2 : \(x-1=5-2x\Leftrightarrow3x=6\Leftrightarrow x=2\)(ktm)