PA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 3 2022
\(x^2+x^2-14x+49=169\)
\(\Leftrightarrow2x^2-14x-120=0\)
\(\Leftrightarrow2\left(x^2-7x-60\right)=0\)
\(\Leftrightarrow x^2-7x-60=0\)
Đó bạn
PA
3
9 tháng 4 2022
triệt tiêu căn x dưới mẫu thì còn căn x trên tử thôi
HN
5 tháng 4 2022
\(\dfrac{-2m+1}{2}=1-2m\) \(\Leftrightarrow\) m=\(\dfrac{1}{2}\).
\(\dfrac{m-1}{2}=m-1\) \(\Leftrightarrow\) m=1.
Hai phương trình đã cho không là hai phương trình tương đương.
PA
2
8 tháng 3 2022
\(\Leftrightarrow x^2+44x-40x-1760=0\)
\(\Leftrightarrow x\left(x-40\right)+44\left(x-40\right)=0\)
\(\Leftrightarrow\left(x+44\right)\left(x-40\right)=0\Leftrightarrow x=40;x=-44\)
PA
1
12 tháng 4 2022
\(a\sqrt{a}+\sqrt{a}+a+1\)
\(=\sqrt{a}\left(a+1\right)+\left(a+1\right)\)
\(=\left(a+1\right)\left(\sqrt{a}+1\right)=\left(a+1\right)\left(1+\sqrt{a}\right)\)
Đặt \(\sqrt{a}\) ra đó bạn
AD
1
13 tháng 6 2023
3: góc AMN=góic ACM
=>AM là tiếp tuyến của đường tròn ngoại tiếp ΔECM
=>góc AMB=90 độ
=>Tâm o1 của đường tròn ngoại tiếp ΔECM nằm trên BM
NO1 min khi NO1=d(N;BM)
=>NO1 vuông góc BM
Gọi O1 là chân đường vuông góc kẻ từ N xuống BM
=>O1 là tâm đường tròn ngoại tiếp ΔECM có bán kính là O1M
=>d(N;tâm đường tròn ngoại tiếp ΔECM) nhỏ nhất khi C là giao của (O1;O1M) với (O) với O1 ;là hình chiếu vuông góc của N trên BM
KV
6 tháng 6 2023
ĐKXĐ: x ≥ 0
Do x ≥ 0 ⇒ √x ≥ 0 và √x + 1 > 0
⇒ 0 ≤ √x < √x + 1
⇒ √x/(√x + 1) < 1
AE
3
7 tháng 6 2023
\(Xét:\dfrac{\sqrt{x}}{\sqrt{x}+1}\) ta thấy rõ ràng : \(\sqrt{x}\ge0\)
\(\Rightarrow\sqrt{x}+1\ge1\)
\(\Rightarrow\sqrt{x}\) không thể : \(\ge\sqrt{x}+1\)
Do đó : \(0< \dfrac{\sqrt{x}}{\sqrt{x}+1}< 1\)
DT
Dang Tung
CTVHS
7 tháng 6 2023
\(\dfrac{\sqrt{x}}{\sqrt{x}+1}\left(ĐK:x\ge0\right)\\ =\dfrac{\sqrt{x}+1}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}\\ =1-\dfrac{1}{\sqrt{x}+1}\)
Ta thấy :
\(1>0,\sqrt{x}+1\ge1>0\forall x\ge0\\ =>\dfrac{1}{\sqrt{x}+1}>0\\ =>-\dfrac{1}{\sqrt{x}+1}< 0\\ =>1-\dfrac{1}{\sqrt{x}+1}< 1\\ =>\dfrac{\sqrt{x}}{\sqrt{x}+1}< 1\)
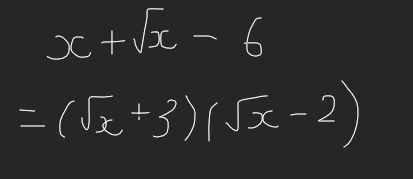
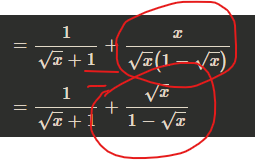
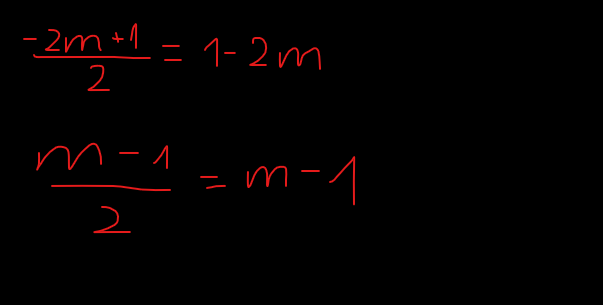
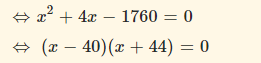
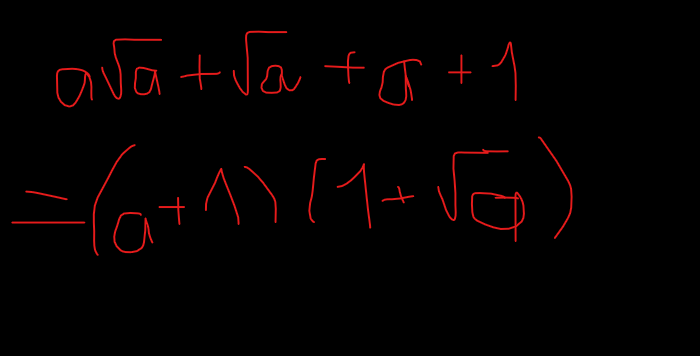
-Đặt \(\sqrt{x}=a\Rightarrow x=a^2\)
\(x+\sqrt{x}-6=a^2+a-6=a^2-2a+3a-6=a\left(a-2\right)+3\left(a-2\right)=\left(a-2\right)\left(a+3\right)=\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)\)