VT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 5 2016
30A=30/2*32+30/3*33+30/4*34=1/2-1/32+1/3-1/33+1/4-1/34=99/100
A=3,3/100
29 tháng 8 2016
a) Tính giá trị của A. Khi x=\(\frac{1}{4}\)là :
\(\frac{\sqrt{\frac{1}{4}}-5}{\sqrt{\frac{1}{4}}+3}=-2,634825932\)
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
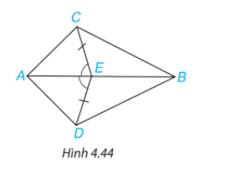
a)Xét hai tam giác AEC và AED có
\(EC = ED\)
\(\widehat {CEA} = \widehat {DEA}\)
AE chung
\( \Rightarrow \Delta AEC{\rm{ = }}\Delta AED\)(c.g.c)
b)
Do \(\Delta AEC{\rm{ = }}\Delta AED\) nên \(\widehat {CAE} = \widehat {DAE}\) ( 2 góc tương ứng) và AC=AD ( 2 cạnh tương ứng).
Xét \(\Delta ABC\) và \(\Delta ABD\) có:
AB chung
\(\widehat {CAE} = \widehat {DAE}\)
AC=AD
\( \Rightarrow \Delta ABC = \Delta ABD\)(c.g.c)
H
7 tháng 8 2023
a)
n = 20 tức n chẵn.
Khi n chẵn: \(A=-4.\dfrac{n}{2}=-4.\dfrac{20}{2}=-40\)
b)
Khi n chẵn:
\(A=-4.\dfrac{n}{2}=-2n\)
Khi n lẽ:
\(A=1+\dfrac{4\left(n-1\right)}{2}=1+2\left(n-1\right)=1+2n-2=2n-1\)
7 tháng 8 2023
a) Số hạng thứ 20 (n=20) là
\(\left(20-1\right).4=76\)
\(A=1-5+9-13+17-21+...+76\)
\(A=\left(-4\right)+\left(-4\right)+\left(-4\right)+...+\left(-4\right)\)
\(A=\left(-4\right).38=-152\)
b) Số hạng thứ n là:
\(\left(n-1\right).4\)
\(\)\(A=1-5+9-13+17-21+...+\left(n-1\right).4\)
\(A=\left(-4\right)+\left(-4\right)+\left(-4\right)+...+\left(-4\right)\) ((n-1).2 số -4)
\(A=\left(-4\right).\left(n-1\right).2=-8\left(n-1\right)\)
và 
. Tính giá trị của biểu thức 
. B. 
. C. 
. D. 
.
.
đạt giá trị nhỏ nhất là 
. B. 
. D. 
.
.
. B. 
. D. 
/
thỏa mãn 
B. 
C. 
D. 
?
5 tháng 8 2019
\(P=...\)
\(=\frac{1}{30}\left(\frac{30}{2.32}+\frac{30}{3.33}+...+\frac{30}{1973.2003}\right)\)
\(=\frac{1}{30}\left(\frac{1}{2}-\frac{1}{32}+\frac{1}{3}-\frac{1}{33}+...+\frac{1}{1973}-\frac{1}{2003}\right)\)
\(=\frac{1}{30}\left[\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{1973}\right)-\left(\frac{1}{32}+\frac{1}{33}+...+\frac{1}{2003}\right)\right]\)
\(=\frac{1}{30}\left[\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{31}\right)-\left(\frac{1}{1974}+\frac{1}{1975}+...+\frac{1}{2003}\right)\right]\)
5 tháng 8 2019
\(Q=...\)
\(=\frac{1}{1972}\left(\frac{1972}{2.1974}+\frac{1972}{3.1975}+...+\frac{1}{31.2003}\right)\)
\(=\frac{1}{1972}\left(\frac{1}{2}-\frac{1}{1974}+\frac{1}{3}-\frac{1}{1975}+...+\frac{1}{31}-\frac{1}{2003}\right)\)
\(=\frac{1}{1972}\left[\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{31}\right)-\left(\frac{1}{1974}+\frac{1}{1975}+...+\frac{1}{2003}\right)\right]\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 tháng 6 2023
a, A = \(\dfrac{12x-2}{4x+1}\)
2\(x\) - 4 = 0 ⇒ 2\(x\) = 4 ⇒ \(x\) = 4: 2 = 2
Giá trị của A tại 2\(x\) - 4 = 0 là giá trị của A tại \(x\) = 2
A = \(\dfrac{12\times2-2}{4\times2+1}\) = \(\dfrac{22}{9}\)
b, A = 1 \(\Leftrightarrow\) \(\dfrac{12x-2}{4x+1}\) = 1
12\(x\) - 2 = 4\(x\) + 1
12\(x\) - 4\(x\) = 1 + 2
8\(x\) = 3
\(x\) = \(\dfrac{3}{8}\)
c, A \(\in\) Z ⇔ 12\(x\) - 2 ⋮ 4\(x\) + 1
12\(x\) + 3 - 5 ⋮ 4\(x\) + 1
3.(4\(x\) + 1) - 5 ⋮ 4\(x\) + 1
5 ⋮ 4\(x\) + 1
Ư(5) ={-5; -1; 1; 5}
Lập bảng ta có:
| \(4x+1\) | -5 | -1 | 1 | 5 |
| \(x\) | -3/2 | -1/2 | 0 | 1 |
Vậy \(x\) \(\in\) {0; 1}