Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Độ dài đường chéo là \(5\sqrt{2}\left(cm\right)\)

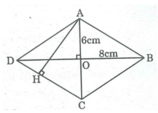
ABCD là hình thoi có O là giao điểm của hai đường chéo nên:
AO = OC = 6cm; OB = OD = 8cm
Trong tam giác vuông OAB, ta có:
A B 2 = O A 2 + O B 2 = 6 2 + 8 2 = 100
AB = 10 (cm)
Kẻ AH ⊥ CD (H ∈ CD)
Ta có: S A B C D = AH.CD ⇒ AH = S A B C D / CD = 96/10 = 9,6 (cm)

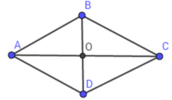
Giả sử hình thoi ABCD có đường chéo AC vuông góc BD tại O, BD = 10 cm; AC = 24 cm.
Suy ra BO = 1 2 BD = 1 2 .12 = 6 (cm);
AO = 1 2 AC = 1 2 .24 = 12 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
AB = A O 2 + B O 2 = 5 2 + 12 2 = 13 (cm)
Đáp án cần chọn là: C

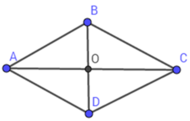
Giả sử hình thoi ABCD có đường chéo AC vuông góc BD tại O, BD = 6 cm; AC = 8 cm.
Suy ra BO = 1 2 BD = 1 2 .6 = 3 (cm);
AO = 1 2 AC = 1 2 .8 = 4 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
AB = A O 2 + B O 2 = 4 2 + 3 2 = 5 (cm)
Đáp án cần chọn là: B


Độ dài cạnh là:
\(\sqrt{\left(\dfrac{3.2}{2}\right)^2+\left(\dfrac{2.4}{2}\right)^2}=2\left(cm\right)\)