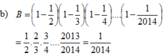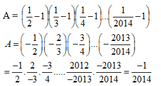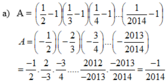Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(S=1-2+2^2-2^3+...+2^{2012}-2^{2013}\)
\(\Rightarrow2S=2-2^2+2^3-2^4+...+2^{2013}-2^{2014}\)
\(\Rightarrow2S+S=2-2^2+2^3-...-2^{2014}+1-2^2-2^3+...-2^{2013}\)
\(\Rightarrow3S=1-2^{2014}\)\(\Rightarrow3S-2^{2014}=1-2^{2015}\)

Bài 1:
Ta có: \(3n+1⋮n-1\)
\(\Leftrightarrow3n-3+4⋮n-1\)
mà \(3n-3⋮n-1\)
nên \(4⋮n-1\)
\(\Leftrightarrow n-1\inƯ\left(4\right)\)
\(\Leftrightarrow n-1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{2;0;3;-1;5;-3\right\}\)(tm)
Vậy: \(n\in\left\{2;0;3;-1;5;-3\right\}\)

a, Áp dụng các t/c các số tận cùng là 1 và 6khi tăng bậc số tận cùng vẫn là 6 và 6.
22015=2.22014=2.41007=2.4.41006=8.16503=8.(...6)=(...8)
32014=91007=9.91006=9.81503=9.(...1)=(...9)
=22015 + 32014 =(...8)+(...9)=(...7)
b, 172023≡72023=7.72022=7.491011=7.49.491010=7.49.2401505=(...3)

Ta có: \(2^1=..2\)
\(2^2=..4\)
\(2^3=..8\)
\(2^4=..6\)
\(2^5=..2\)
\(2^6=..4\)
\(...\)
Lần lượt như vậy, ta sẽ có:
\(2^{4k+1}=..2\)
\(2^{4k+2}=..4\)
\(2^{4k+3}=..8\)
\(2^{4k}=..6\)
Ta có: \(2015=4.503+3\)
\(=>2015=4k+3\)
\(=>2^{2015}=..8\)
Ta lại có: \(3^1=..3\)
\(3^2=..9\)
\(3^3=..7\)
\(3^4=..1\)
\(3^5=..3\)
\(3^6=..9\)
\(...\)
Lần lượt như vậy,ta có quy luật:
\(3^{4k+1}=..3\)
\(3^{4k+2}=..9\)
\(3^{4k+3}=..7\)
\(3^{4k}=..1\)
Ta có: \(2014=4.503+2\)
\(=>2014=4k+2\)
\(=>3^{2014}=..9\)
VẬY: \(2^{2015}+3^{2014}=..8+..9=..7\)
=> \(2^{2015}+3^{2014}\) có tận cùng là 7.
------------------------------------------------------------
Ta có: \(17^1=..7\)
\(17^2=..9\)
\(17^3=..3\)
\(17^4=..1\)
\(17^5=..7\)
\(17^6=..9\)
Lần lượt như vậy, ta có quy luật:
\(17^{4k+1}=..7\)
\(17^{4k+2}=..9\)
\(17^{4k+3}=..3\)
\(17^{4k}=..1\)
TA CÓ; \(2023=4.505+3\)
\(=>2023=4k+3\)
\(=>17^{2023}=..3\)
Vậy \(17^{2023}\) có tận cùng là 3.

a/ \(5^{2014}+5^{2013}-5^{2012}=5^{2012}\left(5^2+5-1\right)=5^{2012}.29⋮29\left(đpcm\right)\)
b/ \(7^{500}+7^{499}-7^{498}=7^{498}\left(7^2+7-1\right)=7^{498}.55⋮11\left(đpcm\right)\)